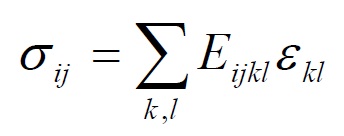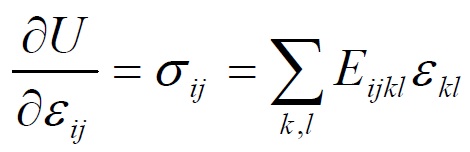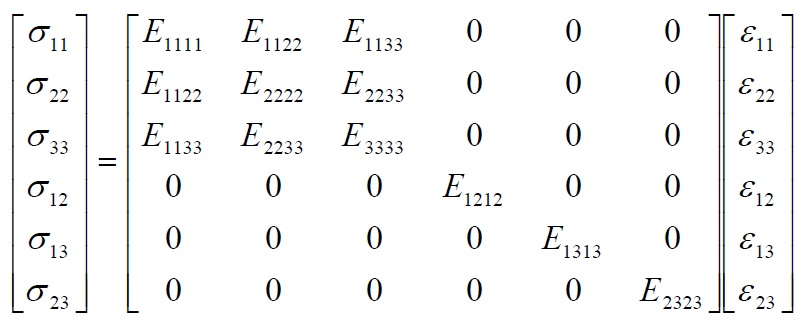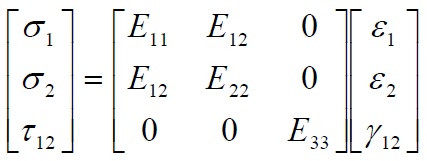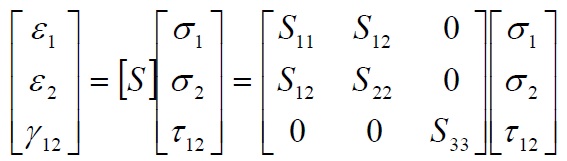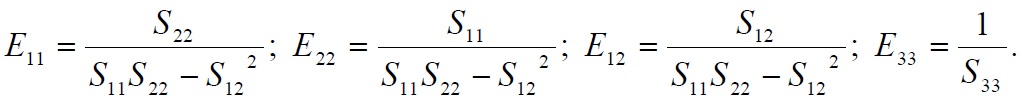1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Matrix of Elasticity
1.4. Matrix of Elasticity
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants
>> Composite Analysis Tool
As is known from the theory of elasticity, the state of tension present in a generic material at around of the point is uniquely described by 9 stress components σij (i, j = 1,2,3). The same applies to the state of deformation, described by the nine components εkl (k, l = 1,2,3). Consequently, the assumption of linear elastic behavior, the relationship between stresses and deformations (generalized Hooke’s law) can be written as:
In the case of fully anisotropic material, the bond stress-deformation, involves 9×9 = 81 elastic constants Eijkl (i, j, k, l = 1,2,3). Since the tensors σij and εkl are symmetric, only 6 components are independent, the independent elastic constants that describe the behavior of an anisotropic material are 6×6 = 36. Thermodynamic considerations also help to reduce furtherly these constants to 21. Indicated with “U” the elastic potential, infact we have that is:
Therefore deriving this with respect to the generic component of deformation εkl we obtain:
Then inverting the order of derivation and taking into account the continuity of U with respect to the functions of deformation, then we get (Schwartz theorem):
Eklij=Eijkl (4)
The ( 4 ) constitute a system of 15 independent equations that allows precisely to reduce constants from 36 to 21 . If the material is orthotropic , ie admits three planes of symmetry mutually orthogonal, then the constitutive laws involving only 9 independent elastic constants. In fact, indicating with 1,2,3 the three principal axes of the material, since the application of σii (i=1,2,3) doesn’t produce distortions εlj (i ≠ j), it must also be:
Eijkl = 0 if k ≠ l (5)
The (5) represents a system of nine equations that allows to reduce the constants from 21 to 12 .
In addition due to the symmetry with respect to the plans 1-2,1-3,2-3 , the application of a shear stress σij (i, j = 1,2,3 and i ≠ j ) does not produce distortion εkl (k ≠ l) in other plans (ij ≠ kl) , ie it must also be:
Eijkl=0 if i ≠j, k ≠ l e ij ≠ kl (6)
For the principle of reciprocity of shear stress (σij = σji) the (6) represents a system of 3 equations that reduces furtherly the elastic constants from 12 to just 9. The elastic constants of an orthotropic material may be advantageously rappresented in a 6×6 symmetric matrix (matrix of elasticity) that allows you to write Hooke’s law in the matrix form :
When we have plane tensions (σ33=σ13=σ23) this relationship can be simplified:
From (8) it is possible, by simple inversion of the matrix of elasticity, obtaining the relationship between stress and strain:
The matrix [S] is called the inverse matrix of elasticity. The significant terms of [S] are related by the terms of the matrix of elasticity by the relations of inversion:
In conclusion the constitutive equations of an anisotropic material involving 21 elastic constants (symmetric matrix 6×6), those of the elastic constants of an orthotropic material 9 (6×6 sparse matrix, see Eq. (7)) that in the case plan reduced to only 4 (3×3 sparse matrices, see eq. (7-8). In any case it has a greater complexity than in the case of isotropic materials that involve, for being two-dimensional and three-dimensional, only two elastic constants (Ε, ν).