Interplanetary flight: 

1) Introduction

2) Heliocentric Transfer Orbit

3) The Gauss Problem

4) Determining Orbital Elements

5) Hyperbolic Departure and Approach

6) Gravitational Assist

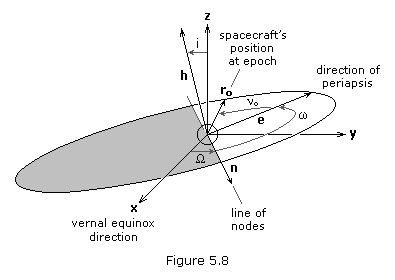
Solving the Gauss problem gives us the position and velocity vectors, r and v, of a spacecraft in a heliocentric-ecliptic orbit. From these vectors we can determine the six orbital elements that describe the motion of the satellite. The first step is to form the three vectors, h, n and e, illustrated in Figure 5.08.

The specific angular momentum, h, of a satellite is obtained from

It is important to note that h is a vector perpendicular to the plane of the orbit.

The node vector, n, is defined as

From the definition of a vector cross product, n must be perpendicular to both z and h. To be perpendicular to z, n would have to lie in the ecliptic plane. To be perpendicular to h, n would have to lie in the orbital plane. Therefore, n must lie in both the ecliptic and orbital planes, or in their intersection, which is called the “line of nodes.” Specifically, n is a vector pointing along the line of nodes in the direction of the ascending node. The magnitude of n is of no consequence to us; we are only interested in its direction.

The third vector, e, is obtained from

Vector e points from the center of the Sun (focus of the orbit) toward perihelion with a magnitude exactly equal to the eccentricity of the orbit.

Now that we have h, n and e we can preceed rather easily to obtain the orbital elements. The semi-major axis, a, and the eccentricity, e, follow directly from r, v, and e, while all the remaining orbital elements are simply the angles between two vectors whose components are now known. If we know how to find the angle between two vectors the problem is solved. In general, the cosine of the angle, , between two vectors a and b is found by dividing the dot product of the two vectors by the product of their magnitudes.

Of course, being able to evaluate the cosine of an angle does not mean that we know the angle. We still have to decide whether the angle is smaller or greater than 180 degrees. The answer to this quadrant resolution problem must come from other information in the problem as we shall see.

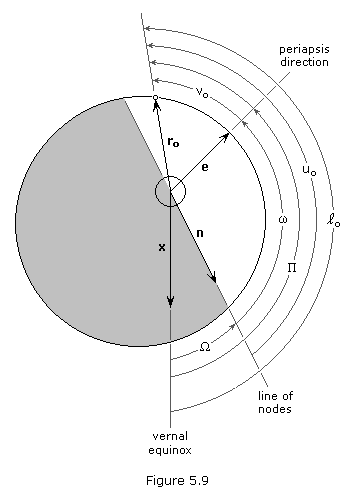We can outline the method of finding the orbital elements as follows:

• Calculate a and e,

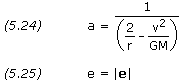
• Since i is the angle between z and h,

(Inclination is always less than 180^o)

• Since 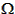 is the angle between x and n,

(If n_y> 0 then  is less than 180^o)

• Since 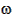 is the angle between n and e,

(If e_z > 0 then is less than 180^o)

• Since _o is the angle between e and r,

(If r •v > 0 then_o is less than 180^o)