Orbit Meccanics:
- 1) Conic Sections
- 2) Orbital Elements
- 3) Types of Orbits
- 4) Newton’s Laws of Motion and Universal Gravitation
- 5) Uniform Circular Motion
- 6) Motions of Planets and Satellites
- 7) Launch of a Space Vehicle
- 8) Position in an Elliptical Orbit
- 9) Orbit Perturbations
- 10) Orbit Maneuvers
The orbital elements discussed at the beginning of this section provide an excellent reference for describing orbits, however there are other forces acting on a satellite that perturb it away from the nominal orbit. Theseperturbations, or variations in the orbital elements, can be classified based on how they affect the Keplerian elements. Secular variations represent a linear variation in the element, short-period variations are periodic in the element with a period less than the orbital period, and long-period variations are those with a period greater than the orbital period. Because secular variations have long-term effects on orbit prediction (the orbital elements affected continue to increase or decrease), they will be discussed here for Earth-orbiting satellites. Precise orbit determination requires that the periodic variations be included as well.
Third-Body Perturbations
The gravitational forces of the Sun and the Moon cause periodic variations in all of the orbital elements, but only the longitude of the ascending node, argument of perigee, and mean anomaly experience secular variations. These secular variations arise from a gyroscopic precession of the orbit about the ecliptic pole. The secular variation in mean anomaly is much smaller than the mean motion and has little effect on the orbit, however the secular variations in longitude of the ascending node and argument of perigee are important, especially for high-altitude orbits.
For nearly circular orbits the equations for the secular rates of change resulting from the Sun and Moon are
Longitude of the ascending node:
![]()
Argument of perigee:
![]()
where i is the orbit inclination, n is the number of orbit revolutions per day, and ![]() and
and ![]() are in degrees per day. These equations are only approximate; they neglect the variation caused by the changing orientation of the orbital plane with respect to both the Moon’s orbital plane and the ecliptic plane.
are in degrees per day. These equations are only approximate; they neglect the variation caused by the changing orientation of the orbital plane with respect to both the Moon’s orbital plane and the ecliptic plane.
Perturbations due to Non-spherical Earth
When developing the two-body equations of motion, we assumed the Earth was a spherically symmetrical, homogeneous mass. In fact, the Earth is neither homogeneous nor spherical. The most dominant features are a bulge at the equator, a slight pear shape, and flattening at the poles. For a potential function of the Earth, we can find a satellite’s acceleration by taking the gradient of the potential function. The most widely used form of the geopotential function depends on latitude and geopotential coefficients, Jn, called the zonal coefficients.
The potential generated by the non-spherical Earth causes periodic variations in all the orbital elements. The dominant effects, however, are secular variations in longitude of the ascending node and argument of perigee because of the Earth’s oblateness, represented by the J2 term in the geopotential expansion. The rates of change of ![]() and
and ![]() due to J2 are
due to J2 are
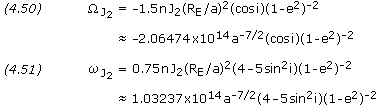
where n is the mean motion in degrees/day, J2 has the value 0.00108263, RE is the Earth’s equatorial radius, a is the semi-major axis in kilometers, i is the inclination, e is the eccentricity, and ![]() and
and ![]() are in degrees/day. For satellites in GEO and below, the J2 perturbations dominate; for satellites above GEO the Sun and Moon perturbations dominate.
are in degrees/day. For satellites in GEO and below, the J2 perturbations dominate; for satellites above GEO the Sun and Moon perturbations dominate.
Molniya orbits are designed so that the perturbations in argument of perigee are zero. This conditions occurs when the term 4-5sin2i is equal to zero or, that is, when the inclination is either 63.4 or 116.6 degrees.
Drag is the resistance offered by a gas or liquid to a body moving through it. A spacecraft is subjected to drag forces when moving through a planet’s atmosphere. This drag is greatest during launch and reentry, however, even a space vehicle in low Earth orbit experiences some drag as it moves through the Earth’s thin upper atmosphere. In time, the action of drag on a space vehicle will cause it to spiral back into the atmosphere, eventually to disintegrate or burn up. If a space vehicle comes within 120 to 160 km of the Earth’s surface, atmospheric drag will bring it down in a few days, with final disintegration occurring at an altitude of about 80 km. Above approximately 600 km, on the other hand, drag is so weak that orbits usually last more than 10 years – beyond a satellite’s operational lifetime. The deterioration of a spacecraft’s orbit due to drag is called decay.
The drag force FD on a body acts in the opposite direction of the velocity vector and is given by the equation
where CD is the drag coefficient, ![]() is the air density, v is the body’s velocity, and A is the area of the body normal to the flow. The drag coefficient is dependent on the geometric form of the body and is generally determined by experiment. Earth orbiting satellites typically have very high drag coefficients in the range of about 2 to 4. Air density is given by the appendix Atmosphere Properties.
is the air density, v is the body’s velocity, and A is the area of the body normal to the flow. The drag coefficient is dependent on the geometric form of the body and is generally determined by experiment. Earth orbiting satellites typically have very high drag coefficients in the range of about 2 to 4. Air density is given by the appendix Atmosphere Properties.
The region above 90 km is the Earth’s thermosphere where the absorption of extreme ultraviolet radiation from the Sun results in a very rapid increase in temperature with altitude. At approximately 200-250 km this temperature approaches a limiting value, the average value of which ranges between about 600 and 1,200 K over a typical solar cycle. Solar activity also has a significant affect on atmospheric density, with high solar activity resulting in high density. Below about 150 km the density is not strongly affected by solar activity; however, at satellite altitudes in the range of 500 to 800 km, the density variations between solar maximum and solar minimum are approximately two orders of magnitude. The large variations imply that satellites will decay more rapidly during periods of solar maxima and much more slowly during solar minima.
For circular orbits we can approximate the changes in semi-major axis, period, and velocity per revolution using the following equations:
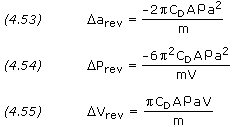
where a is the semi-major axis, P is the orbit period, and V, A and m are the satellite’s velocity, area, and mass respectively. The term m/(CDA), called the ballistic coefficient, is given as a constant for most satellites. Drag effects are strongest for satellites with low ballistic coefficients, this is, light vehicles with large frontal areas.
A rough estimate of a satellite’s lifetime, L, due to drag can be computed from
![]()
where H is the atmospheric density scale height. A substantially more accurate estimate (although still very approximate) can be obtained by integrating equation (4.53), taking into account the changes in atmospheric density with both altitude and solar activity.
Solar radiation pressure causes periodic variations in all of the orbital elements. The magnitude of the acceleration in m/s2 arising from solar radiation pressure is
![]()
where A is the cross-sectional area of the satellite exposed to the Sun and m is the mass of the satellite in kilograms. For satellites below 800 km altitude, acceleration from atmospheric drag is greater than that from solar radiation pressure; above 800 km, acceleration from solar radiation pressure is greater.
PROBLEM 4.16 Calculate the perturbations in longitude of the ascending node and argument of perigee caused by the Moon and Sun for the International Space Station orbiting at an altitude of 400 km, an inclination of 51.6 degrees, and with an orbital period of 92.6 minutes. SOLUTION, Given: i = 51.6 degrees n = 1436 / 92.6 = 15.5 revolutions/day Equations (4.46) through (4.49),Moon = -0.00338 × cos(i) / n
Moon = -0.00338 × cos(51.6) / 15.5
Moon = -0.000135 deg/day
Sun = -0.00154 × cos(i) / n
Sun = -0.00154 × cos(51.6) / 15.5
Sun = -0.0000617 deg/day
Moon = 0.00169 × (4 - 5 × sin2 i) / n
Moon = 0.00169 × (4 - 5 × sin2 51.6) / 15.5
Moon = 0.000101 deg/day
Sun = 0.00077 × (4 - 5 × sin2 i) / n
Sun = 0.00077 × (4 - 5 × sin2 51.6) / 15.5
Sun = 0.000046 deg/day
PROBLEM 4.17 A satellite is in an orbit with a semi-major axis of 7,500 km, an inclination of 28.5 degrees, and an eccentricity of 0.1. Calculate the J2 perturbations in longitude of the ascending node and argument of perigee. SOLUTION, Given: a = 7,500 km i = 28.5 degrees e = 0.1 Equations (4.50) and (4.51),J2 = -2.06474×1014 × a-7/2 × (cos i) × (1 - e2)-2
J2 = -2.06474×1014 × (7,500)-7/2 × (cos 28.5) × (1 - (0.1)2)-2
J2 = -5.067 deg/day
J2 = 1.03237×1014 × a-7/2 × (4 - 5 × sin2 i) × (1 - e2)-2
J2 = 1.03237×1014 × (7,500)-7/2 × (4 - 5 × sin2 28.5) × (1 - (0.1)2)-2
J2 = 8.250 deg/day
PROBLEM 4.18 A satellite is in a circular Earth orbit at an altitude of 400 km. The satellite has a cylindrical shape 2 m in diameter by 4 m long and has a mass of 1,000 kg. The satellite is traveling with its long axis perpendicular to the velocity vector and it's drag coefficient is 2.67. Calculate the perturbations due to atmospheric drag and estimate the satellite's lifetime. SOLUTION, Given: a = (6,378.14 + 400) × 1,000 = 6,778,140 m A = 2 × 4 = 8 m2 m = 1,000 kg CD = 2.67 From Atmosphere Properties,= 2.62×10-12 kg/m3 H = 58.2 km Equation (4.6), V = SQRT[ GM / a ] V = SQRT[ 3.986005×1014 / 6,778,140 ] V = 7,669 m/s Equations (4.53) through (4.55),
arev = (-2 ×
× CD × A ×
× a2) / m
arev = (-2 ×
× 2.67 × 8 × 2.62×10-12 × 6,778,1402) / 1,000
arev = -16.2 m
Prev = (-6 ×
2 × CD × A ×
× a2) / (m × V)
Prev = (-6 ×
2 × 2.67 × 8 × 2.62×10-12 × 6,778,1402) / (1,000 × 7,669)
Prev = -0.0199 s
Vrev = (
× CD × A ×
× a × V) / m
Vrev = (
× 2.67 × 8 × 2.62×10-12 × 6,778,140 × 7,669) / 1,000
Vrev = 0.00914 m/s Equation (4.56), L ~ -H /
arev L ~ -(58.2 × 1,000) / -16.2 L ~ 3,600 revolutions