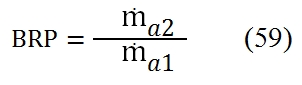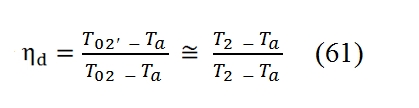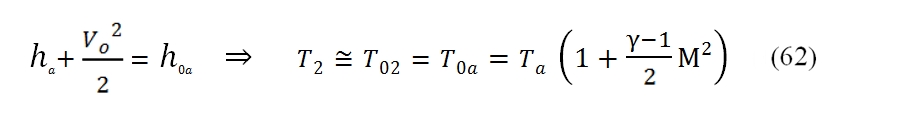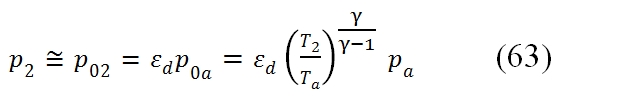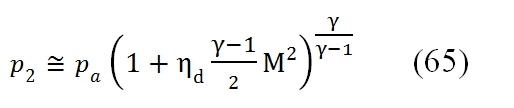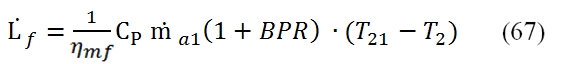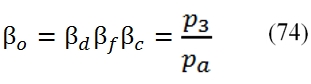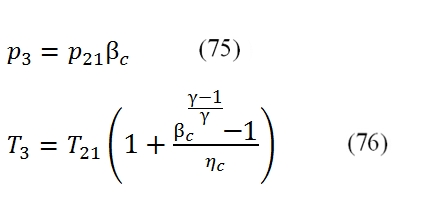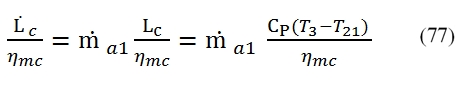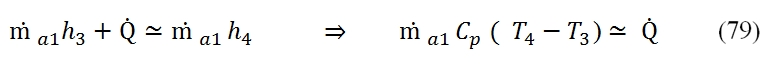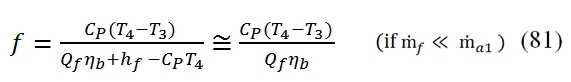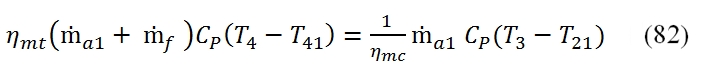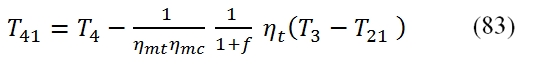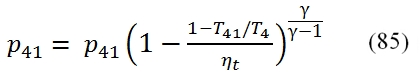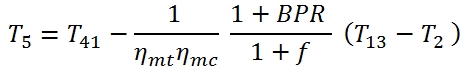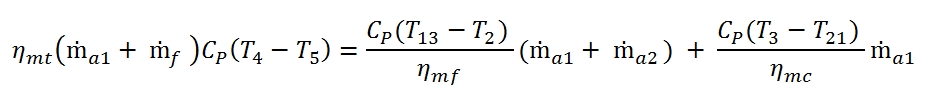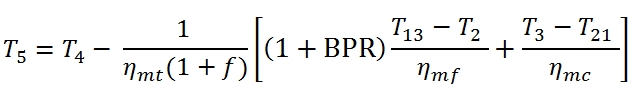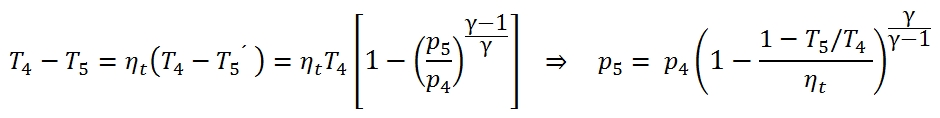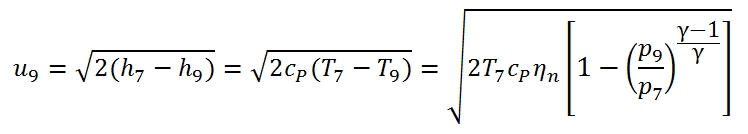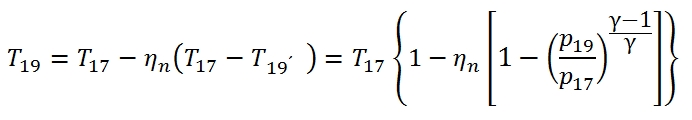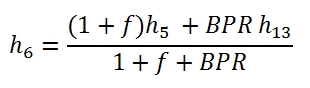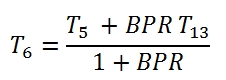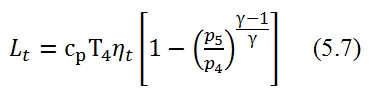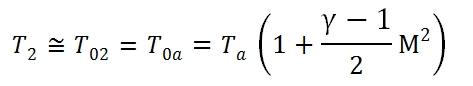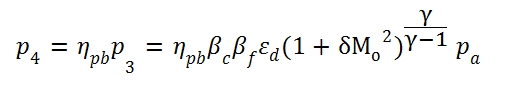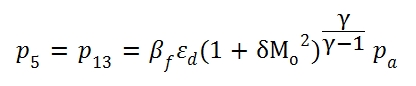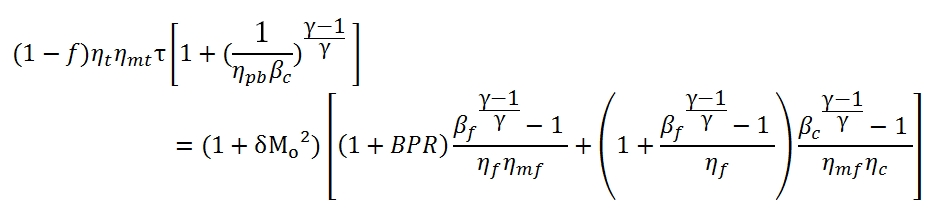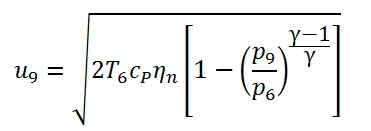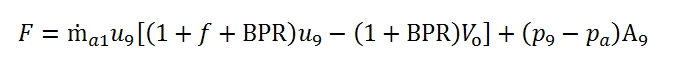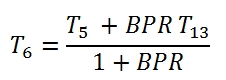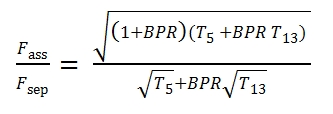1 – Introduction
2 – Aerodinamic for compressible gas – Basic principles
4 – Turbogas cycle
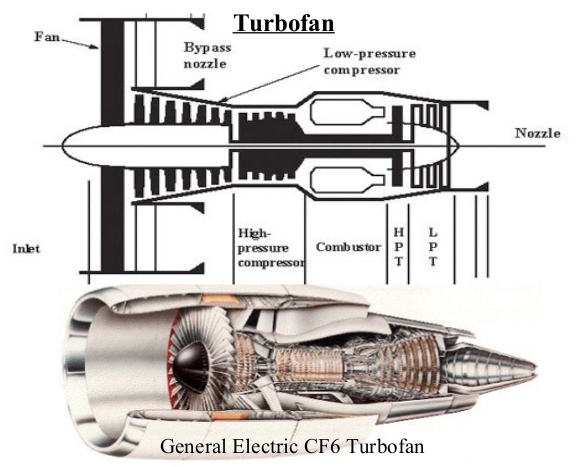
5 – Turbofan
5.1 Turbofan with separated flows
5.2 Turbofan with associated flows
6 – Combustion chamber
7 – Inlet
8 – Nozzle
9 – Turbine Engine
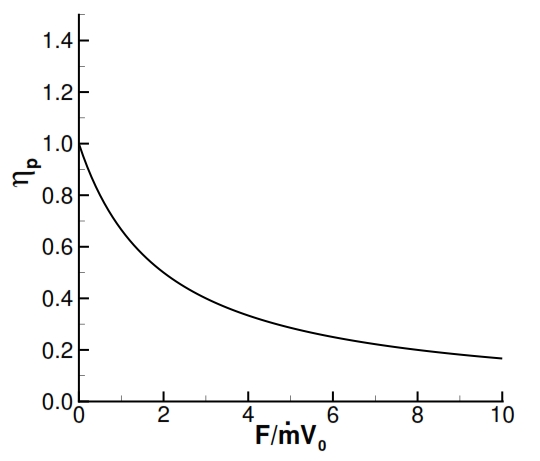
The turbofan is an engine based on the cycle gas turbine, and wherein the available work is directly converted into kinetic energy to generate thrust. The reasons that led to the introduction of the turbofan with respect to the turbojet are principally connected to the efficiency propulsion for an assigned flight velocity and thrust. As explained in paragraph 3, the propulsive efficiency augments by increments of ṁa:
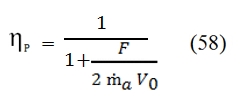
By this formula and the figure 26, is evident that to obtain an higher efficiency is convenient to obtain the required thrust by means small acceleration with an high air flow rate.
Thus the propulsive efficiency ηp can be increased by reducing the specific thrust F/ ṁa, i.e. keeping the same thrust, increasing the air flow rate and deacreasing the effluent velocity (ue). Nevertheless this thrust reduction has some costs:
- Weight: it must be considered, combustor and turbine capable of develop a greater air flow, and therefore heavier.
- Thermodynamic efficiency: the reduction of ue determines a reduction of useful work for each unit mass produced by the cycle. This can be possible by two methods: a) keeping fixed βc and by reducing τ, determining a reduction of ηth; b) keeping fixed τ and using a value of βc far from that one with maximum efficiency, hence determining a reduction of ηth.
To avoid penalizing the basic cycle (ηth), one possibility is the extracting the energy provided at downstream of the turbojet turbine in order to move a second turbine which gives power to a second air flow. This is the principle exploited, albeit in different ways, by the turbofan and the turboprop.
In a turbofan, the energy available at the turbine outlet is not used to accelerate the whole the propulsive fluid, but a part is used in a second turbine that drives a fan that allows to make a limited compression to another current of air (secondary propulsive fluid), then accelerated in a nozzle. In this manner also prevents the whole air flow should pass through the turbomachinery (compressor and turbine), the weight of which can therefore be smaller with values similar to those of the corresponding simple turbojet.
Unlike the turboprop, the secondary air in the turbofan passes inside the motor, although not through the generator of hot gases. The flow contributes to the secondary thrust in that, after being compressed by the fan, It may be expanded till environment pressure and so accelerated to greater velocity than that of air, thus providing its own contribution to the thrust. Since the primary flow passes through the combustor to reach high temperatures, it is also named hot flow, as opposed to the secondary flow also known as cold since it does not feed any process combustion.
The presence of two distinct flows generates the possibility of two different configurations: turbofan with separated flows and with associated flows.
5.1 Turbofan with separated flows
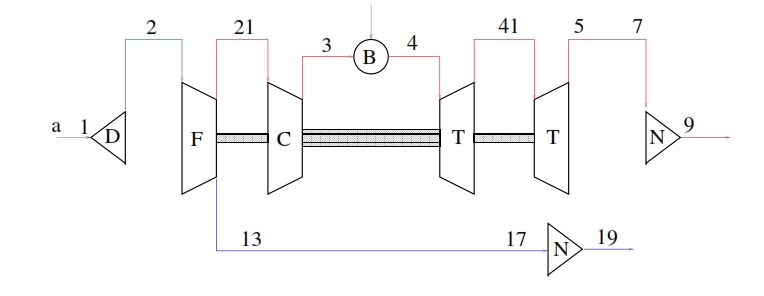
A schematic representation of a turbofan with separated flows is illustrated in Fig. 27. At downstream of diffuser (D), in common to the overall air flow rate (primary and secondary), there are one or more compression stages which build up the fan (F), they are invested by the entire air flow rate as well. Thus are reached the conditions set by the stations 21 for the main flow and 13 for the secondary flow. From this point the two flows follow different paths. In particular, the secondary flow will not be further compressed, and then the conditions at downstream in 13 are equal to at downstream of the last compressor 19 for the secondary flow. The primary flow will instead further compressed by the compressor (C) that develops an higher compression ratio, because characterized by more stages. Consequently, for the primary flow can be considered a first primary compression that takes place in the fan (which leads to the conditions 21). Then the primary flow evolves till to the station 41, where there is the exit of the first turbine. The first turbine provides the power required to move the compressor C. The combustion gases at downstream of the first turbine, with high temperature and with pressure that is still higher than atmospheric, are further expanded in the second turbine, which provides the power needed to move the fan.
At downstream of the second turbine the main flow will be accelerated in the nozzle, exploiting the fraction of useful power still available. Also the secondary flow, downstream of the fan, it may be accelerated in a nozzle. Sometimes when rate of secondary flux is relevant, to save weight, the nozzle is sited just after the fan.
Important parameters are the compression ratio of fan βf and the bypass ratio BRP:
Where ṁa1 and ṁa2 are respectively the primary air flow rate and secondary air flow rate.
5.1.1 Cycle calculation
The thermodynamic conditions of the main flow and the secondary flow can be represented in the plane T – s. In Fig. 28 is reported the most general case of cycle for a real turbofan with separated flows. In the study of the evolution in the plane T – s is important to note that the different transformations refer to different flow rates.
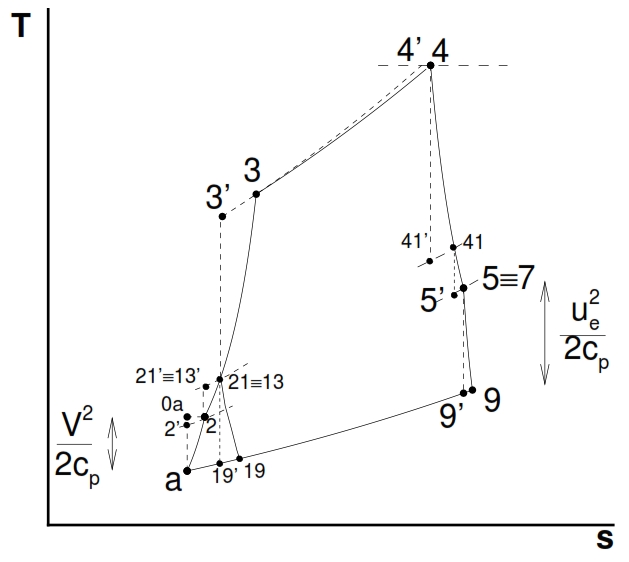
Fig 28: Thermodynamic evolution of the primary and secondary flows in a turbofan with separate flows.
Below we analyze the different transformations shown in Fig. 28 and Fig 27 to obtain the conditions at each station within the engine.
Inlet or Dynamic intake
The purpose of the Inlet is to lead the air into the engine, slowing it down, and increase the static pressure p with minimal losses of total pressure p. It is a component without moving parts, and therefore does not exchange work with the flow; also (at least ideally) not c’`e exchange heat with the outside. Then, as the nozzle, the Inlet or dynamic intake does not exchange energy with the outside but simply transforms, however while the nozzle converts thermal energy into kinetic energy, the Inlet converts kinetic energy into thermal energy. Thus in the Inlet we have:
- The total temperature is constant
- The total pressure decreases (in the real case)
- The static pressure increases
- The cinetic energy decreases
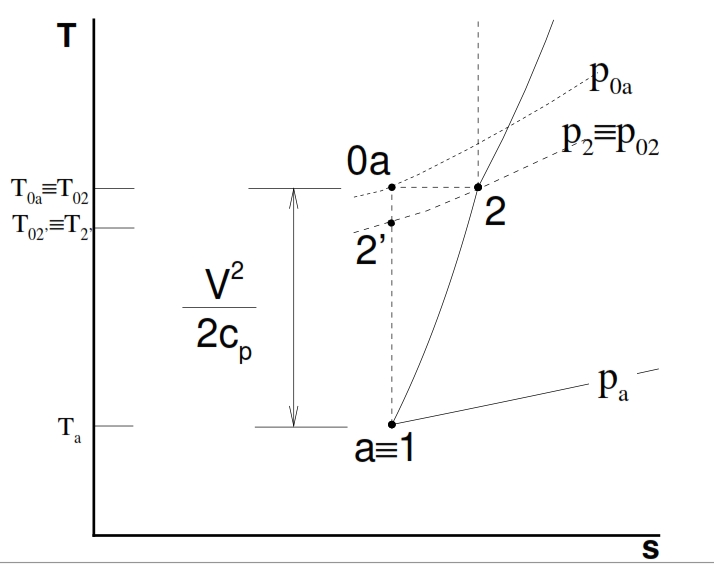
To calculate the conditions of flow downstream of the Inlet can be useful the chart in Fig. 29. Assuming that a low Mach number at outlet of the Inlet, by using the equation of conservation of energy, we have h2, that means the point 2 in the graph will be in the same position of 0a point on the vertical axis, that represents the conditions of stagnation of the current at upstream of the air intake. If the slowdown in the dynamic intake would be isentropic, the conditions at the exit would be equal to the condition of the flow that invests the engine (2 ≡ 0a). The static pressure at downstream of the dynamic intake is then in any case practically coincident with the local total one (for low Mach number of the outlet flux), in particular in the ideal case it is equal to p0a shown in the figure below.
In reality however the total pressure will be more low due to irreversibility of the slowdown, and therefore the point 2 will be at the position shown in Fig. 29, characterized by the same temperature as the point 0a (being the adiabatic process, and the Mach number is low at output ), but at a lower value of total pressure, and highest entropy. To quantify the magnitude of irreversible processes in a dynamic real-Inlet, you can use two different definition of efficiency (by the way, you can calculate from one to the other):
- Ratio of total pressures εd. It is ‘the criterion more intuitive, as it indicates the ratio between the total pressure at the exit of the Inlet and the maximum potentially available, corresponding to an isentropic slowdown: εd=p02/p0a (60)
- Adiabatic efficiency ηd. . This criterion, widely used, is similar with the definition of efficiency adopted for the compressor. Whilst in the case of the compressor is considered the ratio between final pressure and initial one, for the Inlet it depends of the ratio of enthalpy through it (it is equal to V02/2 if the Mach number is low) and the ratio between the outlet pressure and the input pressure (that depends how the ideal transformation approximates the real one). This efficiency can be defined as a ratio of enthalpy (‘ideal’ divided by the real one, to parity of pressure drop). We consider it a transformation from the point “a” (ambient conditions) to the point 2´ (exit for the ‘ideal’ Inlet), “ideal” (thus at constant entropy in the point “a”), which ends in a point (2 ‘, precisely) whose pressure p2´ , is equal to p2 obtained at the end of real transformation. This efficiency can be saw as the ratio of the kinetic energy of the flow at the entrance of the dynamic hold sufficient to reach the pressure p2 if isentropic, and the kinetic energy of the flow at the entrance of Inlet required to reach p2 in the real case:
where the last term of the equation obviously is possible by only to a low Mach number at output of the Inlet. For the conditions at downstream of the Inlet for the temperature we have by the equation of conservation of energy:
while for the pressure you can use one of the performance parameters of the Inlet: if it is known the ratio of total pressures εd you:
While if is known the adiabatic efficiency ηd, by usign the (61), for the T2´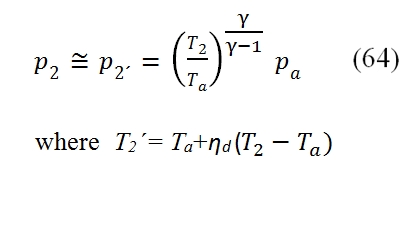 where T2 comes from (62), thus finally we can write:
where T2 comes from (62), thus finally we can write:
This transformation regards the secondary and the primary flows.
Fan or low pressure Compressor
The transformation from point 2 to 21≡13 regards the entire flow mass rate (secondary and primary), and it is characterized by a low compressor ratio βf . The power needed to obtain the required compressor ratio βf can be calculated by this equation:
Where the ηmf is the mechanical efficiency of the fan. By the variation of enthalpy (as function of the variation of temperature) we have:
Where the flow mass rate is expressed by the bypass ratio BPR. The variation of the enthalpy is linked to adiabatic efficiency ηf :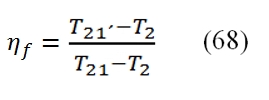 With βf :
With βf :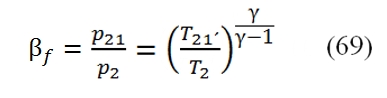
By means these equation can be calculated the performances in 21≡13 as function of βf and ηf :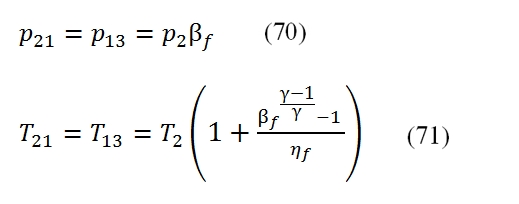
High pressure Compressor
Through it only the principal flow rate passes. The compression ratio can be calculated by this formula:
Another important parameter is the total compression ratio :
then there is the overall compression ratio of the turbofan cycle, that take into account the compression occurs in the Inlet by βd = p2/pa :
At outlet of the compressor we can calculate the pressure and the temperature by these formulas:
Where ηc is the compression efficiency; the absorbed power can be deducted by this equation:
Combustor
The aim of the Combustor is to increase the flux temperature; this occurs by the release of the chemical energy provided by the combustion, that occurs by introducing fuel in the air flux. Only the principal flux goes through the Combustor. The difference between the conditions at downstream and at upstream of combustor can be evaluated by the energy conservation equation, the the variation of the total enthalpy is equal to the energy furnished to the flux (since the external work is nil). The enthalpy balance (referred to the unit time) can be write: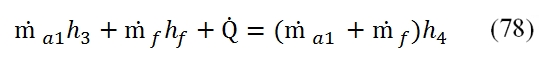
The enthalpy of the flux in the entrance of the Combustor takes into account of the initially enthalpy of the air flux at downstream of the compressor (ṁa1h3), and that one of the fuel (ṁfhf); in the combustion chamber is generated the heat Q (in the equation is expressed per unit time). This energy at the exit of the combustion chamber is distributed to exhaust flow rate, and it is equal to the sum of the air flow rate and fuel flow rate.
The equation (78) can be simplified by neglecting the fuel flow rate, thus in this case we can write:
Where the Cp is supposed constant throught the Combustor (even if the increment of temperature is relevant in the combustion chamber). The heat reluased by the combustion depends by flow rate of the fuel, the heat capacity of the fuel Qf (energy per unit mass) and by the combustion efficiency ηb: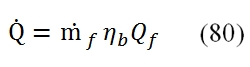 The equations (79) and (80) are used to calculate the ratio f between the fuel flow rate (ṁf) and the air flow rate (ṁa1) needed to reach the temperature at output T4 , that is the maximum temperature allowable in the Turbine (allowable by turbine blade). In the turbogas cycle is convenient to reach a maximum temperature T4. Thus the f = ṁf / ṁa1 is equal to:
The equations (79) and (80) are used to calculate the ratio f between the fuel flow rate (ṁf) and the air flow rate (ṁa1) needed to reach the temperature at output T4 , that is the maximum temperature allowable in the Turbine (allowable by turbine blade). In the turbogas cycle is convenient to reach a maximum temperature T4. Thus the f = ṁf / ṁa1 is equal to:
where is used the (78) and (79). Once the temperature in the point 4 is fixed, can be calculated the ratio air /fuel, but to determine the point 4 is needed another state variable, the pressure p4. This state variable can be deducted by the fact that the adding of heat to a flux with low velocity can occur, without exchanging heat externally, at constant total pressure. In the realty the adding of heat implies a decreasing of total pressure, as more as is high the the flux velocity (or the Mach number). Moreover for others irreversibilities or loss, the total pressure through the Combustor is not constant, therefore to evaluate the pressure at downstream of the combustor can be used the combustor pneumatic efficiency ηpb=p4 / p3, hence by this equation can be calculated the pressure p4.
Compressor Turbine (high pressure turbine)
This turbine provides power to the compressor. To calculate the conditions at downstream of the high pressure turbine, it is used the equation of the power balance:
In this equation has been introduced the mechanical efficiency ηmc (it is the balance between the high pressure compression and turbine high pressure) and . The first member is the power developed by the high pressure turbine available (without the mechanical losses), and the second power requested to the shaft by the compressor. This equation allows you to calculate the temperature at the exit of the turbine (point 41) as follow:
To calculate the pressure we use the adiabatic efficiency ηt by means we can calculate the T41´, and by the isentropic relationship the pressure p41, thus: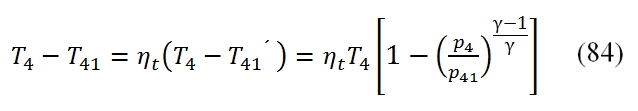
by means is obtainable the pressure at outlet of turbine:
In this case we made the assumption that the efficiencies of both turbines (low and high pressure) are equal (ηt1= ηt2, ηmt1= ηmt2).
Fan Turbine (low pressure turbine)
The calculation of the downstream conditions in the fan turbine it may be carried out similarly to that of the high pressure turbine. In this case the equation of the power balance (the power provided to the turbine with low pressure has to be equal to that requested by the fan):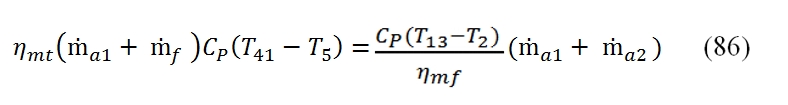
Where T13=T21 , and the mechanical efficiency could be different with respect the case of high pressure Turbine, as well as the adiabatic efficiency. It is relevant to point out that even if the compression ratio of the fan βf could be much lower than βc, the power absorbed by the fan is relevant due to the mass flow rate. By the (86) we can calculate the temperature at the outlet of the turbine as:
To calculate the pressure p5 we have to calculate the T5´ by means the adiabatic efficiency: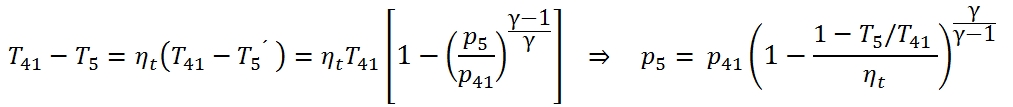
Usually are adopted separate turbines to actuate independently the high-pressure compressor and the fan. This is because the fan, having to develop a bigger flow mass rate, has longer blades compared to the compressor, and therefore it should rotate at a lower speed than the compressor, to contain the efforts due to the centrifugal forces. Thus is adopted a typical configuration “twin-spool”, with two coaxial shafts, the inner one that connects the high-pressure turbine to the compressor, and which rotates at high velocity, and the outer connecting the low-pressure turbine to the fan, which rotates to lower velocities; however basically also is possible to adopt a single turbine to both parts. In this case, the power balance can be written:
By means can be calculated the temperature at outlet of turbine:
To calculate the pressure at outlet can be used the adiabatic efficiency of turbine for the calculation of T5´:
Nozzle of main flow
The main flow, after the second expansion in the turbine, still has an higher pressure than the external environment in order to generate a stream which is expanded until pressure p9, and then expelled to the velocity u9 (the velocity of outflow referred to the station 9). The u9 can be expressed with this equation:
Since the temperature at output can be written as:
5.1.2 Performances
The thrust can be calculated by summation of primary and secondary flows:
From the expression of thrust and considering the jet power as the sum of those relating to each jet we have the following relations:
These expressions can be simplified by introducing the approximation of f << 1 ; it is appropriate to emphasize that the specific thrust was defined as ratio of thrust and air flow totally processed, and it is therefore the relation between the thrust F and the entire air flow rate ṁa1+ ṁa2.
Now we can analyse the behaviour of the performance indexes as function of variation of project parameters.
BRP effect at null flight velocity
In the case of dual-flow turbojet, the specific thrust is referred to the entire flow rate ṁa1+ ṁa2, and it is equal to the average efflux velocity of two flows, calculated proportionally by relative flow rate.
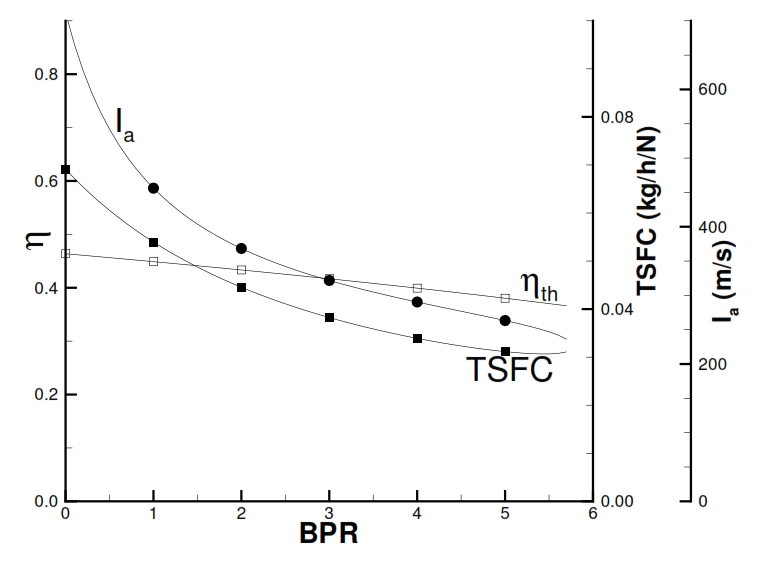
Fig 30: Thermic efficiency, TSFC, and Thrust as function of BPR for a Turbofan with separated flux (βf=1.5, βc=20, Ta=290K, T4=1400K, M=0).
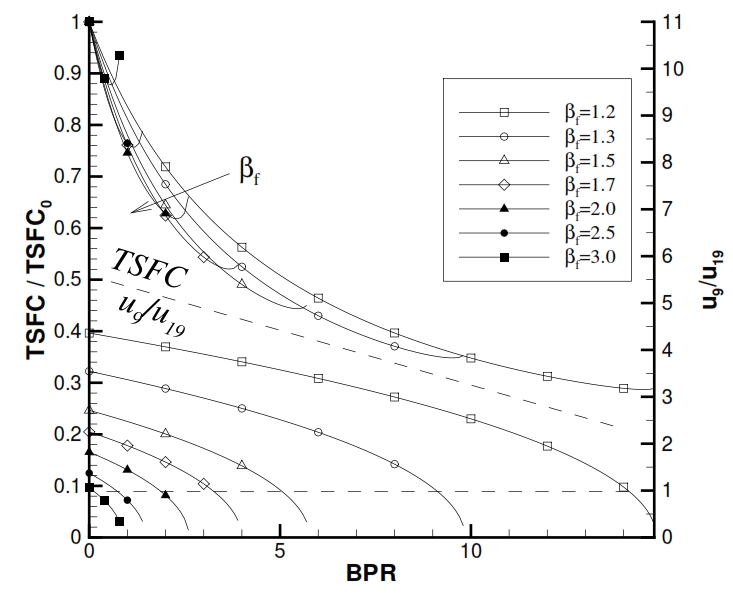
Fig 31: TSFC and u9/u19 as function of βf and BPR for a Turbofan with separated flux (βc=20, Ta=290K, T4=1400K, M=0).
Therefore, if the βf is fixed, by increasing BPR, the specific thrust will decrease (Fig 30), because its value changes from u9,0 (obtained by the available work cp(T41-T9) at downstream of turbine when BPR=0) to average values u9 and u19. It is relevant to point out that for fixed values of βf for the Compressor and the Fan , and for a fixed maximum temperature of the cycle, the ratio F/ ṁa1 (specific thrust referred to the primary flow rate), increases instead with BPR till to reach to the maximum with a maximum value for BPR attainable (i.e. that value attainable by using all the available power for the Fan and so reducing the enthalpic gap for the primary Nozzle till to zero). In the Fig.31 is pointed out that the minimum TSFC is reached when u9/ u19<1 (0.5 in the ideal case), thus when u9 has half value of u19. In the ideal case the thermodynamic efficiency is constant with variation of BPR (infact it depends of βf, βc). In the real case, shown in Fig. 30, the efficiency decrease slightly with BPR, due to lower efficiency of cycle in the case the useful work is converted in kinetic energy passing through the low pressure turbine, Fan and secondary Nozzle (everyone introducing its losses), with respect to the simple Jet where the useful work is converted directly in kinetic energy.
BRP effect during flight
The effects are similar to the case of nill velocity already mentioned (especially for ηt, TSFC, Ia, see figure below).
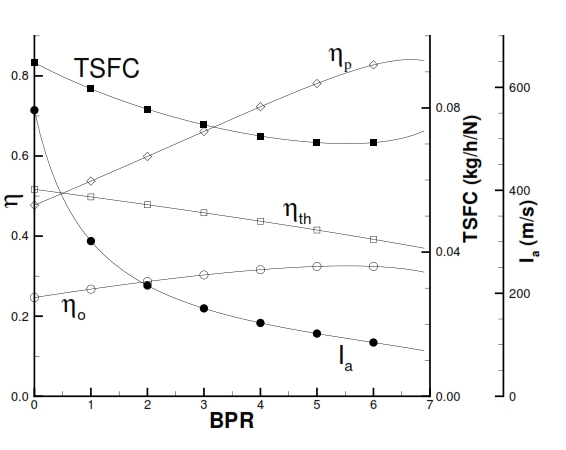
Fig 32: Performance of Turbofan with separated flux by variation of BPR, with βf=1.5; βc=20, Ta=250K, T4=1400K, M=0.8.
But in this case can be considered even the global and propulsive efficiency. The propulsive efficiency ηp depends by difference among the efflux velocities u19 and u9, and the flight velocity Vo , and fixed u19, ηp increases if the u9 decreases, i.e. BPR increases. The global efficiency ηo can be deducted by the specific consumption, by the relation: ηo = Vo / QfTSFC).
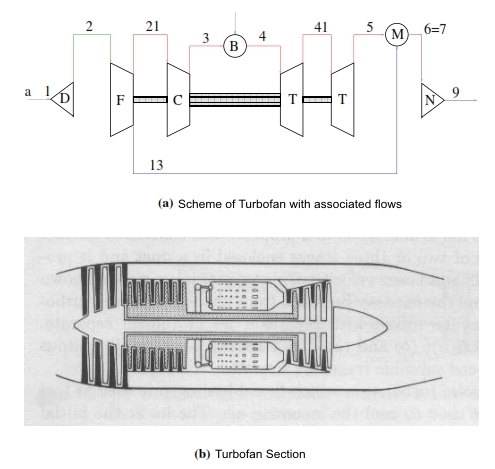
5.2 Turbofan with associated flows
In the Turbofan with separated flows, in the Nozzle, the flow jets have different temperatures. Since, with the same pressure gap, the efflux velocity is proportional to radical square of total temperature of flow, it is possible increase the flow temperature of secondary by using the high temperature of primary flow. On this principle is based the Turbofan with associated flows, which by redistribution of thermic energy and work, it allows to reach better performances with respect that with separated flows, but this advantage has to be evaluated considering the higher weight due to adding of mixer chamber and ducts longer for the secondary flow used for this solution.
In the turbofan with associated flows, the cold flow once it has been compressed in the fan, then it is compressed with the hot flow that outgoing from the Turbine (Fig 33). In the scheme is present another component, the mixer chamber “M”, where the two fluxes can be mixed before to be expanded in the same Nozzle. The fluxes before to enter in the mixer chamber, they have to have the same static pressure, otherwise the flux with higher pressure tend to go in the duct with lower pressure.
5.2.1 Cycle calculation
The calculation of the first part of cycle, till the section 5 for the primary flux, and till section 13 for the secondary flow (Fig. 34), for an assigne value of βf, can be carry out like the Turbofan with separated fluxes. To analyse the differences it is necessary to study the mixer chamber.
Mixer Chamber
For the calculation of the downstream values of mixer chamber with two fluxes, we needs two relations. As already mentioned the two flows have to have the same pressure in the entrance of chamber:![]() The second relation is the conservation of energy, that can be express as enthalpy balance (has to be constant since the flux is essentially adiabatic in the mixer chamber), and i.e. the total entering fluxes have to be equal to the outgoing fluxes (6=position at downstream mixer chamber) :
The second relation is the conservation of energy, that can be express as enthalpy balance (has to be constant since the flux is essentially adiabatic in the mixer chamber), and i.e. the total entering fluxes have to be equal to the outgoing fluxes (6=position at downstream mixer chamber) :![]()
It is important to consider the velocity of the two fluxes, this aspect can have an important influence on the evolution of the flux in the mixer chamber. In this study the fluxes velocity is supposed to be low (we can make this hypothesis since we are in the preliminary project phase), that means the static quantities and stagnation quantities can be considered equal. With this hypothesis the (5.1) is valid for the total pressure, hence it can be calculated p5 once it is assigned βf: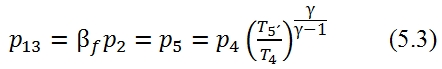
Moreover we can make the hypothesis of ideal mixture, that occurs without losses of total pressures that means:
The (5.3) point out the limitation of pow2er that can be extracted from a turbine of turbofan. Indeed, considering only one turbine that moves the compressor and the fan, the energetic balance can be expressed by this relation:
By means, once is known the efficiencies, compression ratio for fan and compressor, maximum temperature of cycle even for flight conditions, can be used to calculate the only one quantity not known, the BPR. Obviously the same formula can be used to calculate the others parameters if the BPR is known. Hence from the analysis of turbofan with associated fluxes we can point out the following aspects:
- If the value of BPR is given,in order to p5 = p13, the value of βf can not be whatever, but has to be calculated.
- On contrary, if βf is assigned, in order to p5 = p13, the value of BPR can not be whatever, but has to be calculated.
The temperatures at downstream of the mixing of two fluxes can be deducted by the enthalpy balance (5.2) of the mixer, within can approximate the total enthalpy with the static enthalpy, due to the low velocities:
The outcoming enthalpy can be written as:
That with the approximation of f<<1 can be written:
5.2.2 Relation between BPR and βf for Turbofan with associated fluxes and one Turbine
For a turbofan with one turbine, the work produced by the turbine (where for each kilogram of fluid used, we have 1+f kilograms of combustion residues) is used to actuate the fan (where foe each kilogram of fluid we have 1+BPR kilograms of air), therefore the following relation is valid: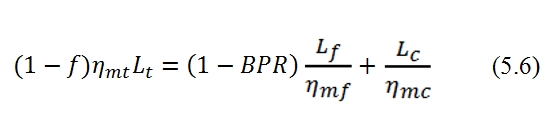
The work in the turbine can be express for each kilogram of air as:
Whilst the work absorbed by the fan and compressor, related to one kilogram of air, can be expressed by the relations:
Where the temperature at the exit of Inlet can be approximated by this following formula:
The ratio p4/p5 used in (5.7) can be calculated by these formulas:
Then for the pressure at incoming of mixer:
Then as consequence we have:
By using this expression in the relation (5.6), and due to τ=T4/Ta, we can write the relation between BPR and βf in a Turbofan with associated fluxes (unique turbine):
By this equation can be calculated βf with an assigned value of BPR, and vice versa.
5.2.3 Performances
For a turbine with associated fluxes, the thrust is calculated by considering the efflux velocity u9 of the unique jet, obtained by the mixing of two flow rates (primary and the secondary one) . The flow rate of the Nozzle is equal to ṁa1(1+f+ BPR) with condition at the entrance of the Nozzle like point 6, and an exit velocity that is depending by pressure, p9 at exit of the Nozzle:
Hence the thrust is equal to:
When the exit pressure is equal to the ambient pressure (p9=pa) and f<<1 the above equation can be reduced to:

Fig 35. Comparison between turfan with associated fluxes and separated with same condition at location 5 and 13.
It is interesting to compare the thrust between the thrust attainable by a Turbofan with separated fluxes and with associated fluxes with the same BPR and βf , with same gas generator (hence with same βc and τ and efficiencies). Both engines have the same conditions in 5 and 13. With the hypothesis of p9=pa the ratio between the thrusts is equal to: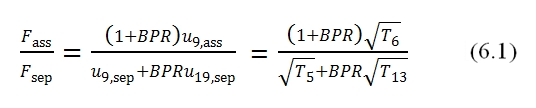
Reminding that T6, T5 and T13 depending by the enthalpy balance in the mixer chamber (5.61) we have:
By using this equivalence, thus the thrust ratio is equal to:
By this equation can be verified when Fass/Fsep > 1, that it is equal to have (Fass/Fsep )2> 1, thus:
This relation is always true (except when the temperature at the exit of turbine is equal to that at the exit of the Fan) . This result highlights, withstanding the assumed hypothesis, it is always convenient to mix the fluxes. Another advantage is the lesser noisy of this solution (it i due to a lesser efflux velocity for the associated fluxes).
With the made hypothesis (f<<1 and p9=pa) the performances quantities can be written as:
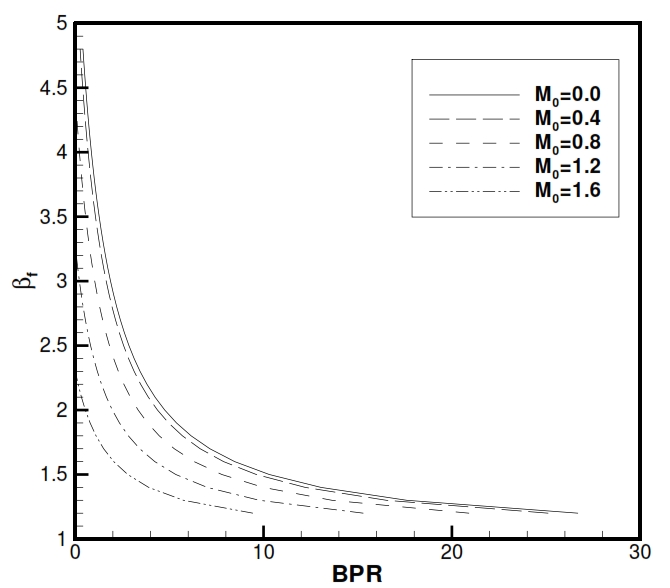
Fig 36. Dependency between βf and BPR for a Turbofan with associated fluxes for differents flight conditions
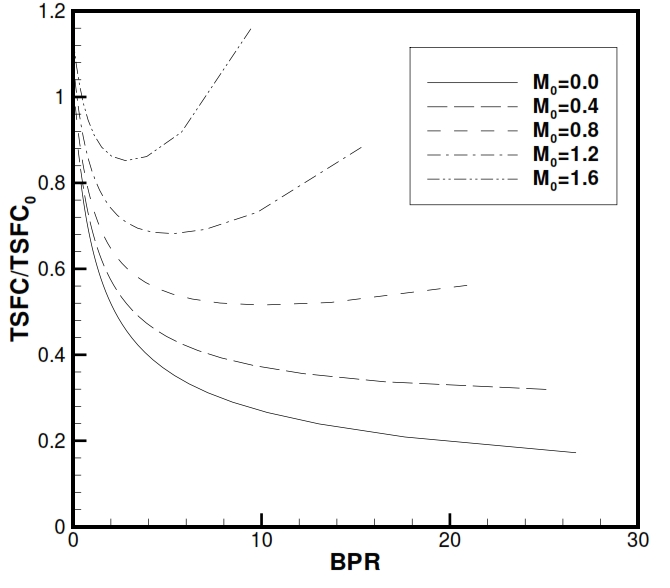
Fig 37. Specific consumption for a Turbofan with associated fluxes with respect a simple jet propulsion (BPR=0), for different flight conditions.
5.3 Advantages and Disavantages of Turbofan
We can consider the following advantages and disadvantages of the Turbofan with respect a simple jet propulsor:
Advantages:
- Higher propulsive efficiency
- Reduction of specific consumption
- Higher autonomy
- Higher thrust at take off
- Lesser noisy (because the noise is proportional to the efflux velocity, that is lesser in the turbofan)
Disadvantages:
- Higher weight: due to higher dimensions of the turbofan
- Higher encumbrance
The choise for the type of turbofan (with separated fluxes or associated) depends of its usage:
– Commercial Vehicles (subsonic flight): the consumption has to be low and then high values of BPR. Generally are considered the separated fluxes and associated fluxes, with a slight preference for the first ones, since they have a lower weight. In case of BPR not so much hight, are preferred the turbofan with associated fluxes, that brings advantages regarding the noisy and consumption.
– Military Vehicles (supersonic flight): are preferred the high thrust usually for this category, and the possibility to install the post-combustion , thus the preference is to use associated fluxes with low BPR.