Rocket Propulsion:
– Thrust
– Combustion & Exhaust Velocity
– Staging
.
In the preceding section we saw that Newton’s second law may be expressed in the form
![]()
Multiplying both sides by dt and integrating from a time t1 to a time t2, we write
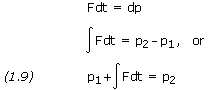
The integral is a vector known as the linear impulse, or simply the impulse, of the force F during the time interval considered. The equation expresses that, when a particle is acted upon by a force F during a given time interval, the final momentum p2 of the particle may be obtained by adding its initial momentum p1 and the impulse of the force F during the interval of time.
When several forces act on a particle, the impulse of each of the forces must be considered. When a problem involves a system of particles, we may add vectorially the momenta of all the particles and the impulses of all the forces involved. When can then write
![]()
For a time interval ![]() t, we may write equation (1.10) in the form
t, we may write equation (1.10) in the form
![]()
Let us now see how we can apply the principle of impulse and momentum to rocket mechanics.
Consider a rocket of initial mass M which it launched vertically at time t=0. The fuel is consumed at a constant rate q and is expelled at a constant speed Ve relative to the rocket. At time t, the mass of the rocket shell and remaining fuel is M-qt, and the velocity is v. During the time interval ![]() t, a mass of fuel q
t, a mass of fuel q![]() t is expelled. Denoting by u the absolute velocity of the expelled fuel, we apply the principle of impulse and momentum between timet and time t+
t is expelled. Denoting by u the absolute velocity of the expelled fuel, we apply the principle of impulse and momentum between timet and time t+![]() t. Please note, this derivation neglects the effect of air resistance.
t. Please note, this derivation neglects the effect of air resistance.
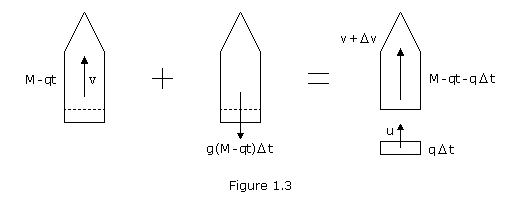
We write
![]()
We divide through by ![]() t and replace u-(v+
t and replace u-(v+![]() v) with Ve, the velocity of the expelled mass relative to the rocket. As
v) with Ve, the velocity of the expelled mass relative to the rocket. As ![]() t approaches zero, we obtain
t approaches zero, we obtain
![]()
Separating variables and integrating from t=0, v=0 to t=t, v=v, we obtain
![]()
which equals
![]()
The term -gt in equation (1.15) is the result of Earth’s gravity pulling on the rocket. For a rocket drifting in space, -gt is not applicable and can be omitted. Furthermore, it is more appropriate to express the resulting velocity as a change in velocity, or ![]() V. Equation (1.15) thus becomes
V. Equation (1.15) thus becomes
![]()
Note that M represents the initial mass of the rocket and M-qt the final mass. Therefore, equation (1.16) is often written as
![]()
where mo/mf is called the mass ratio. Equation (1.17) is also known as Tsiolkovsky’s rocket equation, named after Russian rocket pioneer Konstantin E. Tsiolkovsky (1857-1935) who first derived it.
In practical application, the variable Ve is usually replaced by the effective exhaust gas velocity, C. Equation (1.17) therefore becomes
![]()
Alternatively, we can write
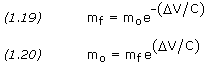
where e is a mathematical constant approximately equal to 2.71828.
For many spacecraft maneuvers it is necessary to calculate the duration of an engine burn required to achieve a specific change in velocity. Rearranging variables, we have
![]()
—————————–
PROBLEM 1.2
The spacecraft in problem 1.1 has an initial mass of 30,000 kg. What is the change
in velocity if the spacecraft burns its engine for one minute?
SOLUTION,
Given: M = 30,000 kg
q = 30 kg/s
Ve = 3,100 m/s
t = 60 s
Equation (1.16),
 V = Ve × LN[ M / (M - qt) ]
V = Ve × LN[ M / (M - qt) ]
 V = 3,100 × LN[ 30,000 / (30,000 - (30 × 60)) ]
V = 3,100 × LN[ 30,000 / (30,000 - (30 × 60)) ]
 V = 192 m/s
V = 192 m/s
PROBLEM 1.3
A spacecraft's dry mass is 75,000 kg and the effective exhaust gas velocity of its
main engine is 3,100 m/s. How much propellant must be carried if the propulsion system
is to produce a total  v of 700 m/s?
SOLUTION,
Given: Mf = 75,000 kg
C = 3,100 m/s
v of 700 m/s?
SOLUTION,
Given: Mf = 75,000 kg
C = 3,100 m/s
 V = 700 m/s
Equation (1.20),
Mo = Mf × e(DV / C)
Mo = 75,000 × e(700 / 3,100)
Mo = 94,000 kg
Propellant mass,
Mp = Mo - Mf
Mp = 94,000 - 75,000
Mp = 19,000 kg
V = 700 m/s
Equation (1.20),
Mo = Mf × e(DV / C)
Mo = 75,000 × e(700 / 3,100)
Mo = 94,000 kg
Propellant mass,
Mp = Mo - Mf
Mp = 94,000 - 75,000
Mp = 19,000 kg
PROBLEM 1.4
A 5,000 kg spacecraft is in Earth orbit traveling at a velocity of 7,790 m/s. Its
engine is burned to accelerate it to a velocity of 12,000 m/s placing it on an escape
trajectory. The engine expels mass at a rate of 10 kg/s and an effective velocity of
3,000 m/s. Calculate the duration of the burn.
SOLUTION,
Given: M = 5,000 kg
q = 10 kg/s
C = 3,000 m/s
 V = 12,000 - 7,790 = 4,210 m/s
Equation (1.21),
t = M / q × [ 1 - 1 / e(DV / C) ]
t = 5,000 / 10 × [ 1 - 1 / e(4,210 / 3,000) ]
t = 377 s
V = 12,000 - 7,790 = 4,210 m/s
Equation (1.21),
t = M / q × [ 1 - 1 / e(DV / C) ]
t = 5,000 / 10 × [ 1 - 1 / e(4,210 / 3,000) ]
t = 377 s