Solutions to make aviation industry turbulence-free
Solutions to make aviation industry turbulence-free Continue reading
How to calculate Weight and Balance -Calculation tool
How to calculate Weight and Balance -Calculation tool Continue reading
AI in the Aerospace Industry
AI in the Aerospace Industry Continue reading
Indian rover begins exploring Moon’s south pole – How it works
Indian rover begins exploring Moon’s south pole Continue reading
An Overview of Drones and their Applications
An Overview of Drones and their Applications Continue reading
The companies racing to make a hypersonic aircraft
The companies racing to make a hypersonic aircraft Continue reading
AI co-pilots are ready to be used on general aviation aircraft
AI co-pilots are ready to be used on general aviation aircraft Continue reading
China’s mysterious space plane returns to Earth after 9-month
China’s mysterious space plane returns to Earth after 9-month Continue reading
NASA tests rotary detonation engine: it will revolutionize space travel
NASA tests rotary detonation engine: it will revolutionize space travel Continue reading
Just 45 Days to Get to Mars by nuclear propulsion, NASA and DARPA will test it soon
Just 45 Days to Get to Mars by nuclear propulsion, NASA and DARPA will test it soon Continue reading
Musk’s Neuralink is now approved for human trials
Musk’s Neuralink is now approved for human trials Continue reading
New kind of solar cells generate electricity even at night
New kind of solar cells generate electricity even at night Continue reading
Startup Made a Functioning ‘Invisibility Shield’. Here’s How It Works
Startup Made a Functioning ‘Invisibility Shield’. Here’s How It Works Continue reading
Researchers make a quantum storage breakthrough by storing a qubit for 20 milliseconds
Researchers make a quantum storage breakthrough by storing a qubit for 20 milliseconds Continue reading
Wind hydrogen, Siemens Gamesa and Strohm collaborate to create a hydrogen transport system produced directly by marine wind turbines
Wind hydrogen, Siemens Gamesa and Strohm collaborate to create a hydrogen transport system produced directly by marine wind turbines Continue reading
Namibia wants to become a green hydrogen superpower
Namibia wants to become a green hydrogen superpower Continue reading
Bill Gates chose where to build his first nuclear plant
It will use the new Natrium technology
Bill Gates chose where to build his first nuclear plant Continue reading
Developed fluorescing composite material that inspects itself
Developed fluorescing composite material that inspects itself Continue reading
The Ultimate Theory of Everything
The Ultimate Theory of Everything Continue reading
New Speed Limit For Moving Quantum Information
New Speed Limit For Moving Quantum Information Continue reading
Technology & Science
Musk's Neuralink is now approv...
Musk's Neuralink is now approved for human trials Read More...
Static Analysis
Lateral Instability of Beam ...
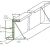Lateral Instability of Beam – Calculation of critical stress value Read More...
Stress Analysis
Inter-Rivet Buckling
Inter-Rivet Buckling Read More...
Aircraft Design
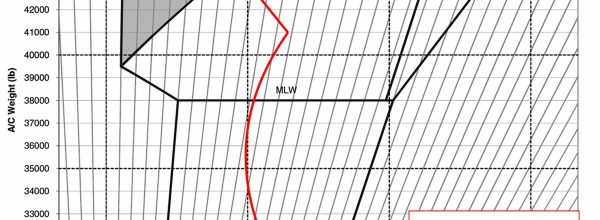
How to calculate Weight and Ba...
How to calculate Weight and Balance -Calculation tool Read More...
podcast
Air Force One: Flying Fortress...
Air Force One: Flying Fortress - Podcast Read More...
Documentaries
Coronavirus Special - Docume...
Coronavirus Special - Documentary 2020 Read More...
FEM - Analysis
How to create Contacts with a ...
For contact simulation between two structural components with MSC Nastran is necessary to perform a static analysis (Linear Simulation by SOL101 Read More...
Space Flight
The Soyuz Launch Sequence Expl...
The Soyuz Launch Sequence Explained Read More...
Propulsion
The Most Launched Rocket - His...
The Most Launched Rocket - History Of The R-7 Read More...
Interplanetary flight
Powering a Starship With a Bla...
Powering a Starship With a Black Hole Read More...
