Rocket Propulsion:
– Thrust
– Combustion & Exhaust Velocity
– Staging
The linear momentum (p), or simply momentum, of a particle is the product of its mass and its velocity. That is,
![]()
Newton expressed his second law of motion in terms of momentum, which can be stated as “the resultant of the forces acting on a particle is equal to the rate of change of the linear momentum of the particle”. In symbolic form this becomes
![]()
which is equivalent to the expression F=ma.
If we have a system of particles, the total momentum P of the system is the sum of the momenta of the individual particles. When the resultant external force acting on a system is zero, the total linear momentum of the system remains constant. This is called the principle of conservation of linear momentum. Let’s now see how this principle is applied to rocket mechanics.
Consider a rocket drifting in gravity free space. The rocket’s engine is fired for time ![]() t and, during this period, ejects gases at a constant rate and at a constant speed relative to the rocket (exhaust velocity). Assume there are no external forces, such as gravity or air resistance.
t and, during this period, ejects gases at a constant rate and at a constant speed relative to the rocket (exhaust velocity). Assume there are no external forces, such as gravity or air resistance.
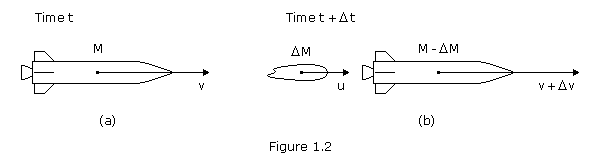
Figure 1.2(a) shows the situation at time t. The rocket and fuel have a total mass M and the combination is moving with velocity v as seen from a particular frame of reference. At a time ![]() t later the configuration has changed to that shown in Figure 1.2(b). A mass
t later the configuration has changed to that shown in Figure 1.2(b). A mass ![]() M has been ejected from the rocket and is moving with velocity u as seen by the observer. The rocket is reduced to mass M-
M has been ejected from the rocket and is moving with velocity u as seen by the observer. The rocket is reduced to mass M-![]() M and the velocity v of the rocket is changed to v+
M and the velocity v of the rocket is changed to v+![]() v.
v.
Because there are no external forces, dP/dt=0. We can write, for the time interval ![]() t
t
![]()
where P2 is the final system momentum, Figure 1.2(b), and P1 is the initial system momentum, Figure 1.2(a). We write
![]()
If we let ![]() t approach zero,
t approach zero, ![]() v/
v/![]() t approaches dv/dt, the acceleration of the body. The quantity
t approaches dv/dt, the acceleration of the body. The quantity ![]() M is the mass ejected in
M is the mass ejected in ![]() t; this leads to a decrease in the mass M of the original body. Since dM/dt, the change in mass of the body with time, is negative in this case, in the limit the quantity
t; this leads to a decrease in the mass M of the original body. Since dM/dt, the change in mass of the body with time, is negative in this case, in the limit the quantity ![]() M/
M/![]() t is replaced by -dM/dt. The quantity u-(v+
t is replaced by -dM/dt. The quantity u-(v+![]() v) is Vrel, the relative velocity of the ejected mass with respect to the rocket. With these changes, equation (1.4) can be written as
v) is Vrel, the relative velocity of the ejected mass with respect to the rocket. With these changes, equation (1.4) can be written as
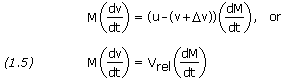
The right-hand term depends on the characteristics of the rocket and, like the left-hand term, has the dimensions of a force. This force is called the thrust, and is the reaction force exerted on the rocket by the mass that leaves it. The rocket designer can make the thrust as large as possible by designing the rocket to eject mass as rapidly as possible (dM/dt large) and with the highest possible relative speed (Vrel large).
In rocketry, the basic thrust equation is written as
![]()
where q is the rate of the ejected mass flow, Ve is the exhaust gas ejection speed, Pe is the pressure of the exhaust gases at the nozzle exit, Pa is the pressure of the ambient atmosphere, and Ae is the area of the nozzle exit. The product qVe, which we derived above (Vrel × dM/dt), is called the momentum, or velocity, thrust. The product (Pe-Pa)Ae, called the pressure thrust, is the result of unbalanced pressure forces at the nozzle exit. As we shall see latter, maximum thrust occurs when Pe=Pa.
Equation (1.6) may be simplified by the definition of an effective exhaust gas velocity, C, defined as
![]()
Equation (1.6) then reduces to
![]()
————————————-
PROBLEM 1.1
A spacecraft's engine ejects mass at a rate of 30 kg/s with an exhaust velocity of
3,100 m/s. The pressure at the nozzle exit is 5 kPa and the exit area is 0.7 m2.
What is the thrust of the engine in a vacuum?
SOLUTION,
Given: q = 30 kg/s
Ve = 3,100 m/s
Ae = 0.7 m2
Pe = 5 kPa = 5,000 N/m2
Pa = 0
Equation (1.6),
F = q × Ve + (Pe - Pa) × Ae
F = 30 × 3,100 + (5,000 - 0) × 0.7
F = 96,500 N