Quantum computing often grabs the headlines. The word “quantum” itself is intriguing enough, and combined with the promise of computational power that surpasses anything we have seen so far it becomes irresistible. But what exactly is quantum computing?
To get to grips with quantum computing, first remember that an ordinary computer works on 0s and 1s. Whatever task you want it to perform, whether it’s calculating a sum or booking a holiday, the underlying process is always the same: an instance of the task is translated into a string of 0s and 1s (the input), which is then processed by an algorithm. A new string of 0s and 1s pops out at the end (the output), which encodes the result. However clever an algorithm might appear, all it ever does is manipulate strings of bits — where each bit is either a 0 or a 1. On the machine level, this either/or dichotomy is represented using electrical circuits which can either be closed, in which case a current flows, or open, in which case there isn’t a current.

The idea of superposition led the physicist Erwin Schrödinger to speculate that a cat in a box could be both dead and alive as long as you don’t look at it. (This cat is definitely alive.)
Quantum computing is based on the fact that, in the microscopic world, things don’t have to be as clear-cut as we’d expect from our macroscopic experience. Tiny particles, such as electrons or photons, can simultaneously take on states that we would normally deem mutually exclusive. They can be in several places at once, for example, and in the case of photons simultaneously exhibit two kinds of polarisation. We never see this superposition of different states in ordinary life because it somehow disappears once a system is observed: when you measure the location of an electron or the polarisation of a photon, all but one of the possible alternatives are eliminated and you will see just one. Nobody knows how that happens, but it does. (You can find out more in Schrödinger’s equation — what is it?)
Superposition frees us of from binary constraints. A quantum computer works with particles that can be in superposition. Rather than representing bits — such particles would represent qubits, which can take on the value 0, or 1, or both simultaneously. “If you do something to [such a quantum system], it’s as though you are doing it simultaneously to 0 and to 1,” explains Richard Jozsa, a pioneer of quantum computing at the University of Cambridge.
Spooky action
You might object that something like superposition could perhaps be achieved using only ordinary classical physics — perhaps by processing two ordinary bits at the same time or something like that — in which case quantum computing wouldn’t be that much more amazing than classical computing. But there is more to quantum physics than just superposition. If you look at a system of more than one qubit, then the individual components aren’t generally independent of each other. Instead, they can be entangled. When you measure one of the qubits in an entangled system of two qubits, for example, then the outcome — whether you see a 0 or a 1 — immediately tells you what you will see when you measure the other qubit. Particles can be entangled even if they are separated in space, a fact that caused Einstein to call entanglement “spooky action at a distance”.
Albert Einstein called entanglement “spooky action at a distance”
Entanglement means that describing a system of several qubits using ordinary classical information, such as bits or numbers, isn’t simply about stringing together the descriptions of the individual qubits. Instead, you need to describe all the correlations between the different qubits. As you increase the number of qubits, the number of those correlations grows exponentially: for n qubits there are 2ncorrelations. This number quickly explodes: to describe a system of 300 qubits you’d already need more numbers than there are atoms in the visible Universe. The idea is that, since you can’t hope to write down the information contained in system of just a few hundred qubits using classical bits, perhaps a computer running on qubits, rather than classical bits, can perform tasks a classical computer can never hope to achieve. This is the real reason why physicists think quantum computing holds such promise.
There’s a hitch however. While a quantum algorithm can take entangled qubits in superposition as input, the output will also usually be a quantum state — and such a state will generally change as soon as you try to observe it. “Nature pulls a trick here,” says Jozsa. “She updates a quantum state, but then she doesn’t allow you to get all the information.” The art of quantum computing is to find ways of gaining as much information as possible from the unobservable.
An example
| Number in decimal | Number in binary |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
An example of a quantum algorithm is one Jozsa developed together with another pioneer of quantum computing, David Deutsch. The task it performs is slightly curious, but we will think of it as follows. Imagine a line of people waiting at the gates of heaven to see whether they’ll be let in. Guarding those gates is Saint Peter who, in deference to his love for computer science, has labelled all the people with numbers written in binary. There happen to be exactly 23 = 8 people, which means that each person gets their own unique string of three 0s and 1s (see the table above for more about binary numbers). Peter records his decisions by allocating a 1 to a particular bit-string if he is going to let the corresponding person in, and a 0 if he’s not. (Technically this allocation is called a Boolean function, a rule which assigns to each bit-string a 0 or a 1. Boolean functions are a staple of computer science, which is why our example isn’t as far-fetched as it may seem at first.)
You don’t know what Peter is going to decide to do with each individual, but you do know that he’s set in his ways: he’ll either let everybody in (every bit-string gets allocated a 1), or he will let exactly half the people in (half of bit-strings get allocated a 0 and the other half a 1). You task is, not to find out what happens to each individual, but whether Peter is in a generous mood and lets everybody in, or whether he is in a grumpy mood, deciding to let only half of the people in. How many values of Peter’s Boolean function do you need to look up to find out which of the two alternatives it is?
If you work like a classical computer, then in the worst-case scenario you’ll have to look the function up five times. That’s because even if you see a 1 allocated to the first 4 bit-strings you check, you still can’t be sure that all the bit-strings come with a 1: there is still the possibility that it’s only half of them, so you do need that 5th look-up. If you have a quantum computer, however, you can get it to look up the function value for all the eight people simultaneously, so you only need one look-up. “For the cost of running the program once with this funny superposition input, you have somehow computed all the [values at once],” explains Jozsa. This advantage of quantum over classical computation becomes even more apparent when there are more people: for a line consisting of 2n individuals, a classical computer would need to look up the function 2n-1+1 times, a number that grows very quickly with n. A quantum computer would always only need to look once.
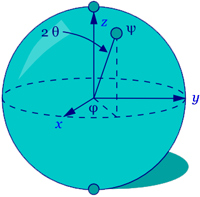
The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.
Will quantum computing take us higher?
But then there is nature’s trick: your eight simultaneously-looked-up values will be encoded in a quantum state you can’t actually read, since any measurement of it will disturb it. Luckily, though, you’re not trying to find out what’ll happen to each individual. You only want to know whether Peter is feeling generous our grumpy. “That’s only one yes-no question,” says Jozsa. “It’s a small amount of information about a lot of values.”
Jozsa and Deutsch showed that it’s possible to perform an extra operation on your quantum state, one which teases the simple piece of information you are after into just the right places for you to be able to read it off. It’s a bit like a house of cards that will collapse as soon as you look at it. You might never be able to see it in its full glory, but if it was constructed in just the right way, you may at least be able to ascertain some information on what it looked like from the collapsed heap. And that’s one reason why quantum computers are more powerful than classical ones. To find even simple patterns or structures within systems of many components a classical computer often has no choice but to first evaluate all, or at least many, of the components individually. A quantum computer, on the other hand, can evaluate all of them simultaneously. And although you may not be able to read off all those individual values, you can often extract just enough information to glean a pattern in them.
Jozsa and Deutsch came up with this algorithm in 1992 and it was the first that could be proven to work exponentially faster than any classical algorithm designed to perform the same task. If you’re imagining Jozsa and Deutsch as quantum engineers tinkering away in a lab, however, you couldn’t be further from the truth. Both of them are theorists. They use the mathematical formalism that describes quantum mechanics and theoretical computer science to work out what a combination of the two can achieve. It’s a purely mathematical endeavour — we’re still some way away from actually building fully functional quantum computers that can perform useful tasks. You can find out more in the following articles:
Quantum Algorithms Will Change Cryptography
Superposition and entanglement are impressive physical phenomena, but leveraging them to do computation requires a very different mindset and programming model. You can’t simply throw your C code on a quantum computer and expect it to run, and certainly not to run faster. Fortunately, mathematicians and physicists are way ahead of the computer builders here, having developed clever algorithms that take advantage of quantum computers decades before the machines started to appear.
Some of the first quantum algorithms created, and honestly, some of the few useful ones I’ve found that you can understand without a graduate degree in math, are for secure cryptographic key distribution. These algorithms use the property of entanglement to allow the key creator to send one of each of many pairs of qubits to the recipient. The full explanation is pretty long, but the algorithms rely on the fact that if anyone intercepts and reads one of the entangled bits en route, the companion qubit at the sender will be affected. By passing some statistics back and forth, the sender and receiver can figure out whether the key was transmitted securely, or was hacked on the way.
You may have read that quantum computers one day could break most current cryptography systems. They will be able to do that because there are some very clever algorithms designed to run on quantum computers that can solve a hard math problem, which in turn can be used to factor very large numbers. One of the most famous is Shor’s Factoring Algorithm. The difficulty of factoring large numbers is essential to the security of all public-private key systems — which are the most commonly used today. Current quantum computers don’t have nearly enough qubits to attempt the task, but various experts predict they will within the next 3-8 years. That leads to some potentially dangerous situations, such as if only governments and the super-rich had access to the ultra-secure encryption provided by quantum computers.
Why Building Quantum Computers Is Hard
There are plenty of reasons quantum computers are taking a long time to develop. For starters, you need to find a way to isolate and control a physical object that implements a qubit. That also requires cooling it down to essentially zero (as in .015 degrees Kelvin, in the case of IBM‘s Quantum One). Even at such a low temperature, qubits are only stable (retaining coherence) for a very short time. That greatly limits the flexibility of programmers in how many operations they can perform before needing to read out a result.
Not only do programs need to be constrained, but they need to be run many times, as current qubit implementations have a high error rate. Additionally, entanglement isn’t easy to implement in hardware either. In many designs, only some of the qubits are entangled, so the compiler needs to be smart enough to swap bits around as needed to help simulate a system where all the bits can potentially be entangled.
Getting Started With Quantum Computing
 The good news is that trivial quantum computing programs are actually pretty easy to understand if a bit confusing at first. Plenty of tutorials are available that will help you write your first quantum program, as well as let you run it on a simulator, and possibly even on a real quantum computer.
The good news is that trivial quantum computing programs are actually pretty easy to understand if a bit confusing at first. Plenty of tutorials are available that will help you write your first quantum program, as well as let you run it on a simulator, and possibly even on a real quantum computer.
One of the best places to start is with IBM’s QISKit, a free quantum toolkit from IBM Q Research that includes a visual composer, a simulator, and access to an actual IBM quantum computer after you have your code running on the simulator. Rigetti Quantum Computing has also posted an easy intro application, which relies on their toolkit and can be run on their machines in the cloud.
Unfortunately, the trivial applications are just that: trivial. So simply following along with the code in each example doesn’t really help you master the intricacies of more sophisticated quantum algorithms. That’s a much harder task.
World’s Largest Quantum Computer Doubles Down
The world’s largest maker of quantum computers, Canada’s D-Wave Systems Inc., recently announced the Pegasus generation of its quantum computers, featuring 2.5 times the qubits (more than 5,000) than its predecessor, as well as the elimination of a major stumbling block to commercialization by directly connecting each of those qubits to three times as many nearby qubits as its previous generation, the Chimera.
Analysts are predicting that Pegasus will advance quantum applications down the technology lifetime exponential growthcurve.
Exemplary applications include Denso Corp.’s automated guided vehicles without collision, T-QARD’s factory optimizationcollaboration with Denso, Volkswagen’s intelligent traffic management application, and Los Alamos National Laboratory’s recent mathematical breakthrough showing how to use D-Wave’s quantum annealing architecture to perform quadratic unconstrained binary optimization in place of supercomputer floating point operations.
“D-Wave’s Pegasus opens up new application horizons,” said Bob Sorensen, chief analyst for quantum computing at Hyperion Research. “By adding over twice as many qubits and three times as many interconnections, the quantum annealing operations performed by Pegasus can be adapted to many other applications besides optimization; from machine learning to financial portfolio risk-assessment.”
“Quantum annealing” describes the hardware architecture used by all D-Wave processors. Quantum annealing sidesteps the need for extensive error correction, a problem that plagues the gate-level implementations of Google, IBM, Microsoft, Rigetti, and Xanadu, limiting them to fewer than 70 qubits. Only Fujitsu has also adopted quantum annealing, albeit in a 1024-bit digital chip that only emulates a quantum computer.
According to Sorensen, D-Wave’s Pegasus topology takes it very close to the threshold of commercial growth by virtue of its vastly improved interconnection matrix, in which each qubit is connected to 15 nearby qubits. “Pegasus bridges the gap between quantum computing and real world of applications,” said Sorensen.
The previous generation, Chimera quantum computers, only made direct interconnections between a qubit and five adjacent qubits, forcing programmers to “waste” some of its 2,000 qubits per chip as makeshift interconnections. The new arrangement will allow all 5,000 qubits to be used for equation variables, enabling complex real-world problems to be solved, according to Sorensen.
“For logistics applications, such as optimally routing taxis to riders and their destinations, Pegasus can now handle far more taxis than before,” said Mark Johnson, vice president of processor design and development of quantum products at D-Wave. “Due to its higher connectivity architecture, equation variables can be represented with far fewer qubits. New applications can be taken closer to a positive return-on-investment [ROI], including route scheduling, financial portfolio optimization, and machine learning.”
D-Wave claims that even though its quantum annealing needs no error correction, Pegasus does have improvements in precision that will make a big difference by shortening run times. Quantum annealing works in a manner similar to semiconductor or metallurgical annealing. It’s an iterative process, and each iteration of the annealing process yields a more precise result, so greater precision at each step greatly decreases the overall run time for a given level of precision.
“The increased number of qubits and interconnections is interesting, but the big deal is Pegasus’ higher precision,” said Matthew Brisse, research vice president at Gartner Inc. “There are already over 100 [Chimera] applications on GitHub, but now programmers can accelerate those and their own algorithms by shifting to the new Pegasus topology.”
According to Brisse, it will take five years or more before true quantum supremacy (the potential ability of quantum computing devices to solve problems that classical computers cannot) will be demonstrated on not just scientific, but also on everyday commercial applications.
The software development environment created by D-Wave, called Leap, is already educating programmers on how to best make the transition to quantum, without needing to learn the underlying physics. Programmer efforts are also being spurred by D-Wave’s Ocean code library with standardized Python and C++ application programmer interfaces (APIs) plus Jupyter Notebooks, which allows interactive changes that instantly update results.
Brisse and Sorensen also praised D-Wave for directly responding to its user base when crafting the new Pegasus topology. Most D-Wave users run their quantum algorithms in the cloud, rather than purchasing the company’s hardware. Luckily, D-Wave has unusually patient funding sources, since it is still getting their full support on its 20th birthday.
D-Wave says it was already leading the world in the sophistication of its superconducting process technology, but claims to have extended that lead with a newly enhanced process technology developed with SkyWater Technology, its microchip fabrication foundry. Not only does its current process offer niobium features below 240 nanometers, but also lowers its on-chip noise level, which for a quantum computer translates to longer coherence times—the length of time before data values collapse from a quantum superposition of states into a digital one or zero state. Thus besides enabling more quantum variables to tackle larger problems, according to D-Wave’s Johnson, Pegasus’ lower noise also enables the solution of more complex problems that require longer coherence times to solve.
Finally, Pegasus directly confronts how classical computers and quantum computers work together as companions, rather than as competitors. According to Johnson, hybrid configurations of classical and quantum computers will off-load to Pegasus only the parts of a problem that run better on quantum computers, while retaining a companion classical computer to run the rest of an application’s algorithms. This hybrid architecture has been built into the latest revisions of Leap and its Ocean algorithm library to simplify quantum programming, as well as to demonstrate the best practices needed to perform hybrid classical-quantum computing.
“We really believe that successful customer solutions will be hybrids, so new operating software enhances hybrid configurations with lower latency and new options for scheduling problems,” said Johnson. “In fact, D-Wave is the only company with real-time qubit scheduling, as well as block-of-time scheduling.”
Real-time qubit scheduling allows algorithms to split up classical and quantum operations on a fine-scale, step by step, while block-of-time scheduling permits quantum and/or classical operations to be continuously executed without the overhead of switching modes.
Michael Cusumano at the Massachusetts Institute of Technology (MIT), who is familiar with programming the Chimera generation, says, “D-Wave’s latest machine and programming environment sounds like real progress, and should be exciting for software developers working in the D-Wave ecosystem. Clearly, there are some significant technical advances, and the latest technology may well be closer to a general-purpose quantum computer.”
D-Wave’s Hybrid, for marrying an in-house classical computer to a cloud-based quantum computer, is available on GitHub, as are many of the Pegasus components. The rest of the Pegasus offerings will be rolled out by the company over the next 18 months, according to Johnson.