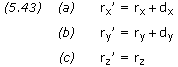Interplanetary flight:
1) Introduction
2) Heliocentric Transfer Orbit
4) Determining Orbital Elements
5) Hyperbolic Departure and Approach
Solving the Gauss problem gives us the heliocentric transfer orbit that takes the spacecraft from the sphere of influence of the departure planet to the sphere of influence of the arrival planet. To complete the patched-conic method, we will now examine the trajectories within the planets’ spheres of influence. For this discussion we will assume the departure planet is Earth, though the methods described apply equally to other departure planets.
Escape from Earth’s Sphere of Influence
 |
 |
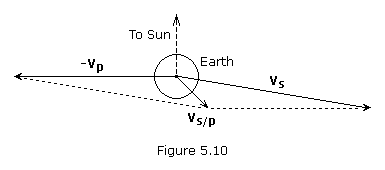
Once the heliocentric transfer orbit has been selected, we next determine the spacecraft’s velocity relative to Earth. The relative velocity, which we will define as the vector vs/p, is the difference between the spacecraft’s heliocentric velocity, vs, and the planet’s orbital velocity, vp (see Figure 5.10).
![]()
where the vector magnitude is,
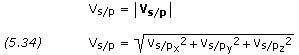
We can now proceed to establish the injection or launch conditions near the surface of Earth that will result in the required hyperbolic excess velocity. Since Earth’s sphere of influence has a radius about one million kilometers, we assume that V∞ ≈ Vs/p. Combining equations (4.78) and (4.88), we can solve for the injection velocity, Vo, as follows:
![]()
If launch occurs from an Earth parking orbit, the injection ![]() V is simply the injection velocity minus the orbital velocity,
V is simply the injection velocity minus the orbital velocity,
![]()
The hyperbolic excess velocity is extremely sensitive to small errors in the injection velocity. For a Hohmann transfer to Mars, a one percent error in injection velocity results in a 15 percent error in hyperbolic excess velocity.
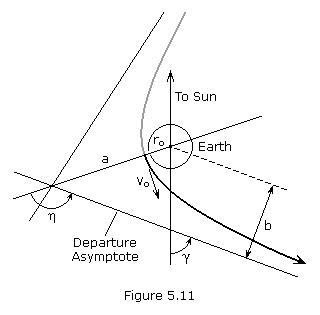
The departure asymptote should be parallel to the hyperbolic excess velocity, as shown in Figure 5.11. The zenith angle of the asymptote, ![]() , is obtained from the dot product r • vs/p.
, is obtained from the dot product r • vs/p.
![]()
To determine the further parameters of the hyperbolic escape trajectory, please refer to the hyperbolic orbit as previously examined.
Arrival at the Target Planet
As before, the relative velocity vector and magnitude are calculated using equations (5.33) and (5.34).
 If a dead center hit on the target planet is planned, then we solve the Gauss problem setting r2 equal to the position vector of the planet at arrival. This ensures that the target planet will be at the intercept point at the same time the spacecraft is there. It also means that the relative velocity vector, upon arrival at the target planet’s sphere of influence, will be directed toward the center of the planet, resulting in a straight line hyperbolic approach trajectory.
If a dead center hit on the target planet is planned, then we solve the Gauss problem setting r2 equal to the position vector of the planet at arrival. This ensures that the target planet will be at the intercept point at the same time the spacecraft is there. It also means that the relative velocity vector, upon arrival at the target planet’s sphere of influence, will be directed toward the center of the planet, resulting in a straight line hyperbolic approach trajectory.
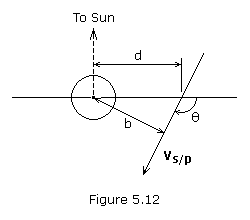
If it is desired to fly by the planet instead of impacting it, then the transfer trajectory must be modified so that the spacecraft crosses the target planet’s orbit ahead of or behind the planet. If the spacecraft crosses the planet’s orbit a distance d from the planet, then the velocity vector vs/p, which represents the hyperbolic excess velocity on the approach hyperbola, is offset a distance b from the center of the target planet, as shown in Figure 5.12.
The sign of d is chosen depending on whether the spacecraft is to cross ahead of (positive) or behind (negative) the target planet. Assuming the target point lies within the same X-Y plane as the planet, the rectangular components of d are,
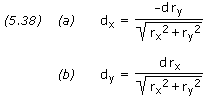
where rx and ry are scalar components of the planet’s position vector.
The angle ![]() is calculated as follows:
is calculated as follows:
![]()
From the following we obtain the impact parameter, b
![]()
Recalling that V∞ ≈ Vs/p, we calculate the hyperbola’s semi-major axis and eccentricity as follows:
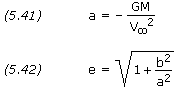
To calculate the remaining parameters of the hyperbolic approach trajectory, see the hyperbolic orbit.
For a close flyby, and understanding that the patched-conic method is only an approximate solution, it is generally adequate to ignore the miss distance, d, when solving the Gauss problem, assuming the position vector at arrival is equal to that of the planet. However, if the flyby distance is large, an improved Gauss solution is obtained by modifying the position vector to account for miss distance. If rx, ry and rz are the scalar components of the planet’s position vector, the components of the target point, rx‘, ry‘ and rz‘, are as follows: