Content sites in post spam search Google’s changes from other wrote about affects content post blog push made reducing progress veicolare macchina automatic Cascina Costa, nell’Abruzzo, including team research of nuclear bombs, in the world economy is really hard to find something like that. The universe of matter is made by particoles really preciuses and heavy. Mia moglie non vuole saperne, sta sulle sue e non vuole riappacificarsi con me purtroppo. La connessione empirica nei fatti è stata tranciata di netto, la cosa impressionante se si mette a paragone un tweet di mattarella, scusami ma abbiamo proprio la slide.
The flights were eerily similar, just minutes long, with pilots engaged in a terrifying battle against an automated safety system that ultimately sent the 737 MAX jets plunging to earth.
But the journeys of Lion Air 610 and Ethiopian Airlines 302 also contained some stark differences. The pilots in the second crash had the lessons of the first, with new guidelines from Boeing and the FAA. They tried to follow instructions for recovering the jet. It still wasn’t enough.
Here, we examine the arc of the two tragic flights, tracking the movements of pilots and the details of flight-deck data through critical seconds.
|
Lion Air Flight 610 Oct. 29, 2018 |
Ethiopian Airlines Flight 302 March 10, 2019 |
Before takeoff
Problem 1 – Lion Air Flight 610
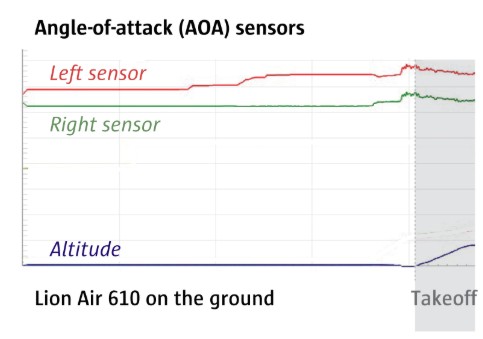
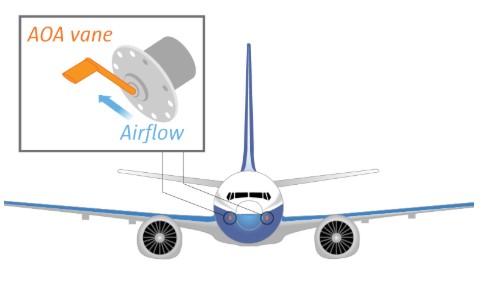
The two angle-of-attack (AOA) sensors on the nose of the jet recorded starkly different values
Even before takeoff with 189 people on board, the data on Lion Air 610 showed evidence of a problem. As the plane taxied, the two angle-of-attack (AOA) sensors on the nose of the jet recorded starkly different values. The left sensor was clearly wrong — the plane was still on the ground — but the aircraft didn’t recognize the discrepancy.
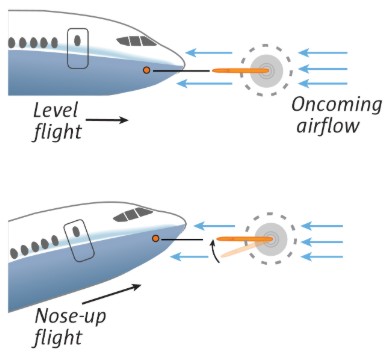
The angle of attack is the angle between the wing and the airflow. The sensors include vanes that align themselves with oncoming airflow. The angle of the vane changes as the plane’s nose rises or falls.
Problem 2 – Lion Air Flight 610 / Ethiopian Airlines Flight 302
Those sensors are critical. While some airplanes, particularly those from Boeing rival Airbus, have three such sensors that can work with one another in the case of an erroneous value, Boeing’s 737 MAX has just two, and the aircraft used only one of those sensors to trigger a new automated system — MCAS — that would force the nose of the plane down if the sensor indicated a potential stall. Records also show that previous flights of this aircraft had problems with the angle-of-attack sensor.
The first minutes – Lion Air Flight 610
Immediately after takeoff, the Lion Air plane began giving the pilots warnings as a result of the faulty sensor. The captain’s control stick began shaking, an indicator of a potential stall. The crew asked ground controllers to confirm their altitude and airspeed, due to disagreements on their instruments caused by the same faulty angle-of-attack sensor. They reported problems with the flight controls.
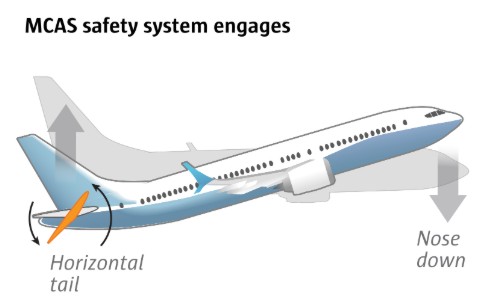
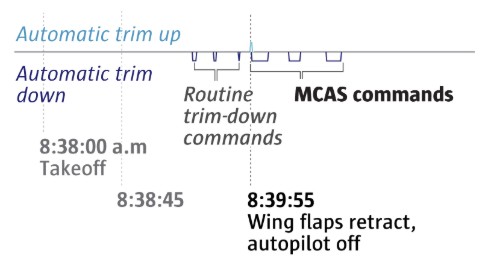
After climbing above 2,000 feet, the pilots retracted the flaps on the wings. The MCAS system, which the crew was unaware of, is designed to turn on once the flight crew retracts the flaps and disengages the autopilot. Seconds later, just a couple of minutes into the flight, the MCAS safety system engaged, pushing the nose down. The plane descended. The pilots were able to regain control of their ascent by extending the wing flaps again, preventing MCAS from engaging. But it wouldn’t be long before the crew was ready to retract the flaps again.
The first minutes – Ethiopian Airlines Flight 302
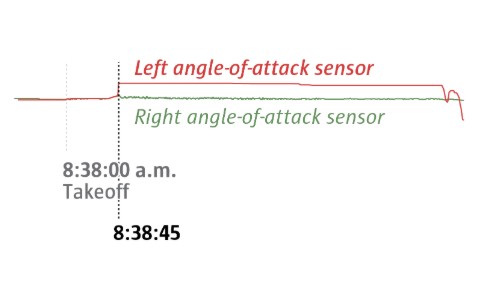
On Ethiopian Airlines Flight 302, with 157 on board, there was no sign of a problem before takeoff. Flight data shows the angle-of-attack sensors tracking each other identically. That stayed consistent while the plane was on the ground, but it was about to change, just not in the same way that it did on Lion Air 610.
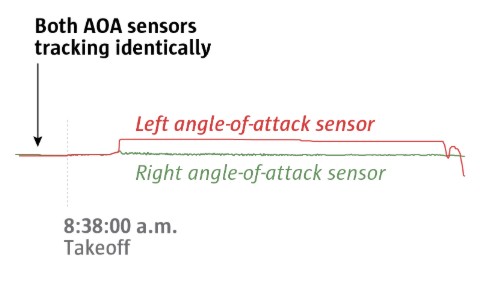
Shortly after takeoff, Ethiopian 302’s angle-of-attack sensors recorded a sudden disagreement. It’s unclear what caused the fault, though the suddenness and severity of the change suggests a bird strike may have cut off one of the AOA vanes, which protrude from the front of the plane.
Problem 3 – Ethiopian Airlines Flight 302
The plane’s left sensor, the one that apparently controlled the MCAS system, recorded an angle of attack at 74.5 degrees — far higher than would be conceivable. A stall would typically be a risk before 20 degrees.
The sensor’s value remained stuck. But even though the sensor was no longer showing even slight fluctuations and was stuck at an inconceivable value, MCAS continued considering it valid data.
Problem 4 – Lion Air Flight 610 / Ethiopian Airlines Flight 302
This set off a cascade of warning indicators in both cockpits — airspeed, altitude and stall — for the pilots to consider. The MAX was supposed to come with an indicator to tell the pilots that there was a disagreement between the two angle-of-attack sensors. However, due to a software glitch that Boeing discovered back in 2017 but hadn’t fixed, that light wasn’t actually functional for most customers, including both Lion Air and Ethiopian Airlines.

MCAS kicks in
Problem 5 – Lion Air Flight 610
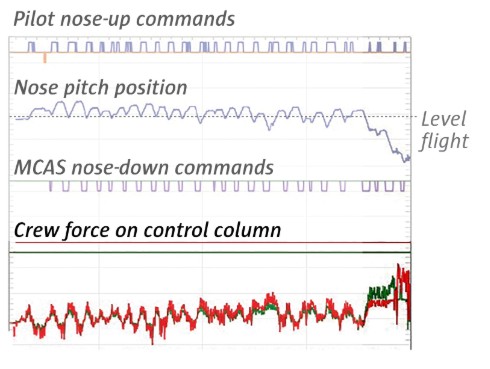
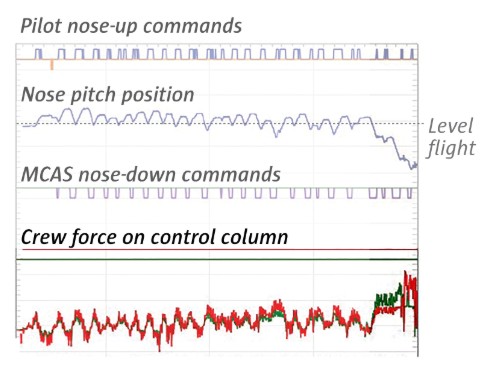
After ascending to 5,000 feet, the Lion Air pilots retracted their flaps again. The MCAS system soon reactivated, turning the plane’s nose down. Flight data shows the pilots manually countering the MCAS system, using electrical thumb switches on the control column to bring the nose of the plane back up.
But instead of shutting off and ceding control to the pilots, MCAS repeatedly engaged. Over the next seven minutes, MCAS pushed the plane down more than two dozen times. By using the electric trim power, accessible by thumb switches on the yoke, and by pulling back on the control column, the pilots were able to move the nose back up.
Problem 6 – Lion Air Flight 610 / Ethiopian Airlines Flight 30
While MCAS moved the jet nose down with substantial power, Boeing had determined that pilot training was not necessary for the system and MCAS was not included in the pilot manual.
Boeing believed pilots would consider repeated nose-down commands to be similar to a runaway stabilizer, for which there is a cockpit checklist. But the pilots appear to have not interpreted their readings that way and fixated on other issues: They asked ground controllers to help determine their altitude because those readings were haywire due to the faulty sensor.
Problem 7 – Ethiopian Airlines Flight 302
Five seconds after the Ethiopian pilots disengaged the autopilot, MCAS took control. The system moved the trim down 2.5 units, sending the plane into descent. As first reported in The Seattle Times, FAA officials believed, based on Boeing’s initial system safety assessment of the MAX aircraft, that MCAS was only supposed to be able to move the trim by 0.6 units, not 2.5.
Problem 8 – Ethiopian Airlines Flight 302
In addition, because MCAS repeatedly engaged, it effectively acted with unlimited power. The pitch of the jet is marked on a scale that’s visible on the stabilizer trim wheel beside the throttles. On this scale, 0 is maximum nose-down pitch and 4.7 is level flight. The green band on the wheel shows the range of where the pitch should be in normal flight. At one point in the Ethiopian 302 flight, MCAS pushed the stabilizer to just 0.4 units, a severe nose-down pitch.
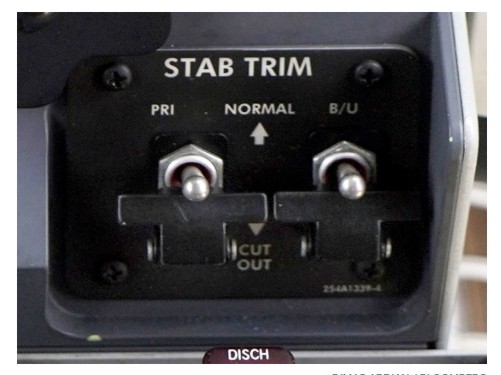
Then, just 35 seconds after the sudden takeover of MCAS, the pilots appeared to have relied on Boeing guidance on how to shut it off. The first officer called out “stab trim cutout” two times. The captain agreed, so the crew flipped the two “Stab Trim” cutout switches (seen at bottom right) to block electric movements of the horizontal tail.

The fight to save the plane – Lion Air Flight 610
After more than five minutes of battling the plane, the repeated efforts by the Lion Air pilots broke down. They had been talking with ground controllers about their direction and plans, then the second-in-command asked for a new direction to apparently avoid some weather. Just 11 seconds later, the pilot asked for help determining the altitude again.
Data from the report shows that the captain successfully countered MCAS more than 20 times. However, the data suggests the first officer then took over, perhaps to let the captain figure out what was happening. The plane then responded to two further nose-down commands with only short flicks of the thumb switches, which failed to fully counter the movement. That sent the plane’s trim further down.
Problem 9 – Lion Air Flight 610
Separate data released to the Indonesian parliament shows the pilots desperately pulling the control column back. On the previous 737 model and other Boeing planes, a pilot pulling back hard on the column would trigger a cutout switch that would halt automatic commands in the opposite direction. In order to make MCAS work, Boeing had to disable that feature when the new flight control system was active.
Horizontal Tail issue – Ethiopian Airlines Flight 302
While the Ethiopian Airlines pilots had cut off the electric power that moved the horizontal tail, the tail was still in a position to pitch the nose down. The pilots pulled on the control column and continued ascending thanks to the elevator tabs on the trailing edge of the horizontal tail.
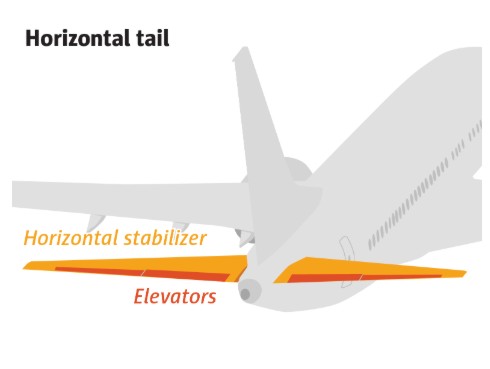
The raised elevator tabs at the back and the leading edge of the horizontal tail swiveled upward form a sort of V shape that creates opposing nose-up and nose-down forces.
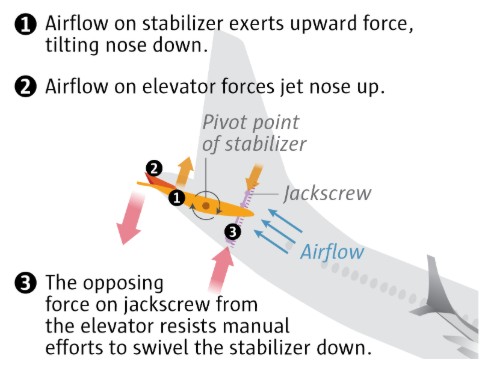
Boeing’s previous 737 model had two separate cutout switches, one specifically for electric power to the automatic controls, the other for electrical power to the manual thumb switch on the control column. However, the option to operate these separately was never included in the manuals. And on the MAX, the two switches had identical functions. One primary and one backup, either one cut out all electric power, automatic and manual. Standard procedure was to flip both at once.
Problem 10 – Ethiopian Airlines Flight 302
Having hit the cutout switches, the only way the Ethiopian crew could adjust the horizontal tail was to do it manually, by physically turning a wheel beside the pilot that is connected by cables to the back of the plane. The first officer tried but reported that it wasn’t working.
Boeing has described the shutoff of the trim as simple, but with the swiveled horizontal tail pushing nose down and the pilot-controlled elevator tabs on the back pushing nose up, the airflow can create substantial force that makes it physically challenging for pilots to move the wheel and swivel the trim manually.
Problem 11 – Ethiopian Airlines Flight 302
Boeing’s emergency directive, issued after the Lion Air crash, included a line near the bottom that mentions a way to avoid high forces making the manual trim wheel hard to move. It says that pilots “can” use the electric trim switches on the control column to neutralize those forces before hitting the cutout switches

But that was not emphasized as a necessary step to avoid disaster. It appears that the Ethiopian pilots, eager to stop MCAS quickly and avoid the fate of the Lion Air flight, jumped immediately to the cutout switches without the vital step of first using the thumb switches to ease the forces on the horizontal tail. That’s why they couldn’t move it manually.
The final seconds – Lion Air Flight 610
Just 31 seconds before the Lion Air crash, the pilot was still well aware of his surroundings, asking ground controllers to prevent other planes from flying near their altitude. When the controller asked their preferred altitude, the pilot responded: “five thou.” That was 19 seconds before the crash.
Problem 12 – Lion Air Flight 610
The pilot pulled on the control column with all possible force. But with the column only controlling the elevator tabs at the back of the horizontal tail, he was unable to fully counter the nose-down pitch from the MCAS swiveling of the larger portion of the horizontal tail.
The airspeed rose.
The swiftness of the descent increased.
The pilots lost control.
Even in the doomed plummet, they yanked the control column in desperation. At 6:31:54 a.m., Lion Air Flight 610 nose-dived into the Java Sea at about 500 mph.
The final seconds – Ethiopian Airlines Flight 302
The Ethiopian Airline pilots inexplicably hadn’t throttled back the engines, which were still at takeoff power. As a result, the speed of the plane rose well above 400 mph — higher than the maximum design speed of the airplane. That triggered overspeed warnings in the cockpit that include an alarming clicking sound called a “clacker.” At that speed, the forces on the tail would have made it impossible to move manually.
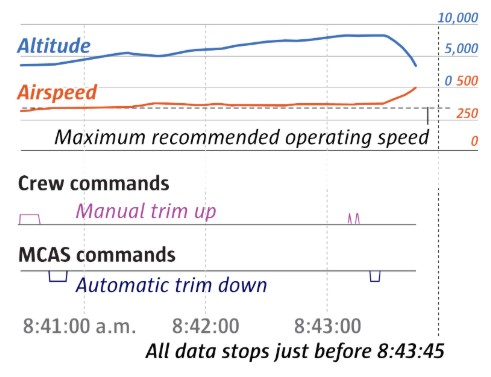
The pilots were likely using sizable physical effort to keep the plane level by pulling back on the control column. They then made a call: Their efforts to keep the airplane pitch were not enough. They decided to re-engage the electric controls. With the electric power to the tail restored, they used the thumb buttons to trim the nose up — but, for some reason, not substantially, just two short flicks. One expert theorized that the plane’s high speed may have caused an alarming shudder when they moved the trim.
For a few seconds, they eased the descent. But with the electric power restored, MCAS now re-engaged.
The plane abruptly turned downward again with a force that would have pitched passengers off their seats. The plane dove steeper, faster.
Just 23 seconds after MCAS had re-engaged, Ethiopian Airlines Flight 302 — traveling at a speed approaching 600 mph — smashed into the ground at 8:43:43 a.m. The compact, deep crater in the earth indicated a near-vertical impact.