Interplanetary flight: 

1) Introduction

2) Heliocentric Transfer Orbit

3) The Gauss Problem

4) Determining Orbital Elements

5) Hyperbolic Departure and Approach

6) Gravitational Assist

 

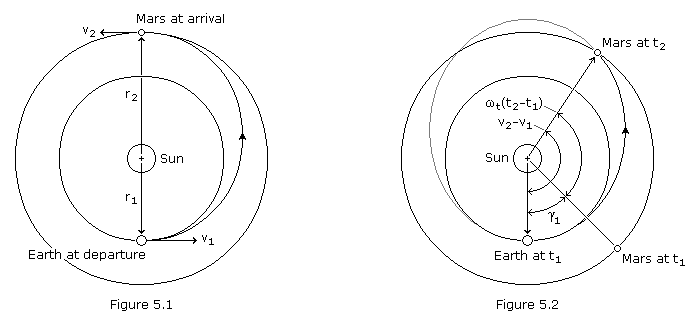
For transfers to most of the planets, we may initially consider that the planetary orbits are both circular and coplanar. In the Orbital Mechanics section of this site we discussed the problem of transferring between coplanar orbits and found that the most economical method, from the standpoint of V required, was the Hohmann transfer. A Hohmann transfer between Earth and Mars is pictured in Figure 5.1 below.

While it is generally desirable that the transfer orbit be tangential to Earth’s orbit at departure, it may be preferable to intercept Mars’ orbit prior to apogee, especially if the spacecraft is to return to Earth. The Hohmann transfer, if continued past the destination planet, would not provide a suitable return trajectory. For a one-way trip this is irrelevant; however, for a probe that is to be recovered or for a manned mission, this consideration is important. The outbound trip to Mars on the Hohmann trajectory consumes between 8 and 9 months. If the spacecraft continued its flight it would return to the original point of departure only to find Earth nearly on the opposite side of its orbit. Therefore, either the spacecraft must loiter in the vicinity of Mars for nearly 6 months or the original trajectory must be modified so that the spacecraft will encounter Earth at the point where it recrosses Earth’s orbit.

If the spacecraft is to encounter the target planet at the time it crosses the planet’s orbit then obviously Earth and the target planet must have the correct angular relationship at departure. The angle between the radius vectors to the departure and arrival planets is called , the phase angle at departure, and is pictured in Figure 5.2 for a Mars trajectory. The total sweep angle from departure to arrival is just the difference in the true anomaly at the two points, ₂–₁.

From Figure 5.2 we can see that the transfer is the one-tangent burn type, which we examined previously. Selecting a transfer orbit allows the determination of the change in true anomaly and the time-of-flight using equations (4.67) and (4.71). The target planet will move through an angle of _t(t₂–t₁) while the spacecraft is in flight, where _t is the angular velocity of the target planet. Thus, the correct phase angle at departure is,

The requirement that the phase angle at departure be correct severely limits the times when a launch may take place. The heliocentric longitudes of the planets are tabulated in The Astronomical Almanac, and these may be used to determine when the phase angle will be correct. Alternatively, the page Planet Positions provides the data and demonstrates the methods necessary to estimate planet positions without needing to refer to other sources.

Mars Transfer Trajectories

The methods described above provide only a very rough estimate of the phase angle, particularly in the case of Mars. The orbit of Mars is significantly eccentric, meaning its angular velocity changes considerably depending on whether it is near perihelion or aphelion at the time of transfer. For a better estimate we can no longer consider the orbit to be circular.

As can be seen from Figure 5.2, the proper alignment for a transfer to Mars occurs in the months just prior to an opposition. The location of Mars within its orbit at the time of opposition depends on the time of year the opposition occurs. Perihelion oppositions occur in the August-September time period, and aphelion oppositions occur in the February-March time period. We can, therefore, link the phase angle required to the time of year that we initiate the transfer.

 

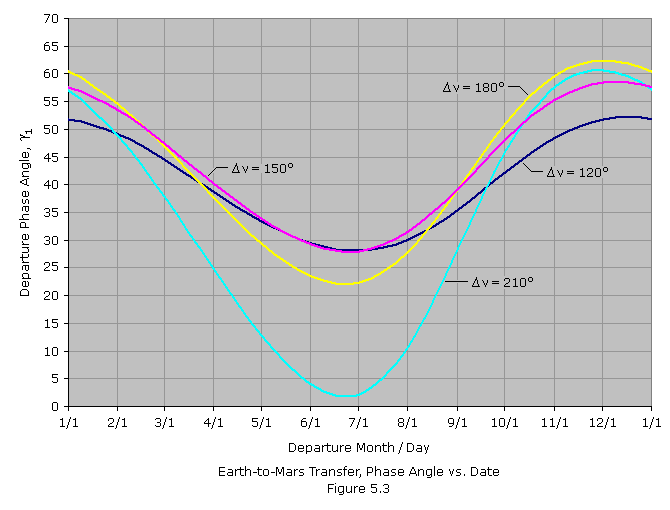
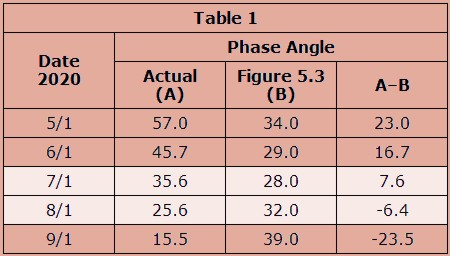
Figure 5.3 above is a chart showing departure phase angle versus departure calendar date. Four curves are shown, each representing a different transfer orbit. The trajectories are tangent to Earth’s orbit at departure and differ in the number of degrees the spacecraft travels around the Sun before intercepting Mars, i.e. the change in true anomaly, . If the interplanetary trajectory carries the spacecraft less than 180 degrees around the Sun, it’s called a Type-I trajectory. If the trajectory carries it 180 degrees or more around the Sun, it’s called a Type-II. A Type-I trajectory is pictured in Figure 5.2. In a Type-II trajectory, the intercept point is at the second Mars orbit crossing.

Figure 5.3 gives the required phase angle for transfers departing on the dates listed across the bottom of the chart. To use Figure 5.3 it is necessary to find the date when the actual phase angle equals the required angle obtained from the chart. For example, let’s say we are planning a mission to launch around the October-13 opposition of the year 2020. It’s decided we’ll use a Type-I trajectory in which the spacecraft’s true anomaly change is 150 degrees (magenta curve). In Table 1 we list the actual Mars-Earth phase angle for the months leading up to the October opposition, along with the phase angle read from Figure 5.3. We see that there is a date in July when the two numbers are equal. We can interpolate that the departure date will be sometime in the third week of July and the departure phase angle will be approximately 30 degrees.

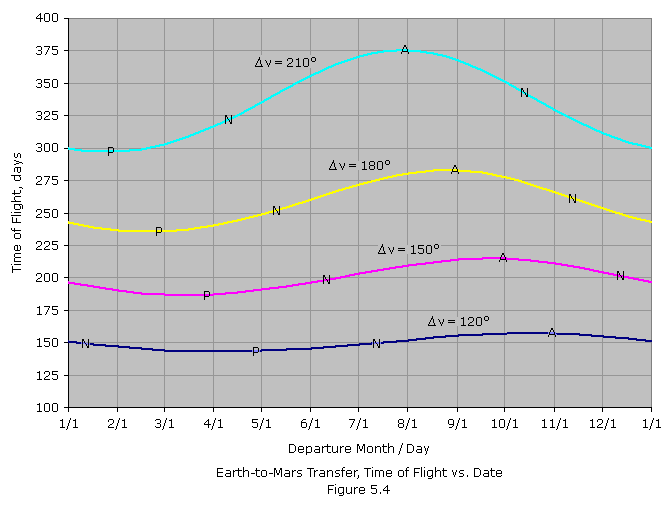
Just as phase angle is dependent on Mars’ location within its orbit, so is the time of flight. After estimating the departure date from Figure 5.3, we can use Figure 5.4 below to estimate the flight duration. For instance, for the July departure window determined above, the time of flight for a trajectory with a true anomaly change of 150^o is found to be about 207 days. The letters superimposed on each curve indicate the departure dates that will result in the spacecraft intercepting Mars at perihelion (P), aphelion (A) or one of the two nodes (N).

 

Referring again Figure 5.2, we see that the flight path angle of the transfer orbit is positive at the first Mars orbit crossing and negative at the second Mars orbit crossing. Therefore, it may be preferable to use a Type-I trajectory when interception occurs with Mars in the part of its orbit past perihelion and approaching aphelion, when the planet’s flight path angle is likewise positive. Conversely, a Type-II trajectory may be preferable when interception occurs with Mars in the part of its orbit past aphelion and approaching perihelion. Having Mars and spacecraft flight path angles both positive or both negative reduces the angle between the velocity vectors, and thus the relative velocity. This can be critical when V is the limiting factor. Of course a Type-I trajectory is always preferable when minimizing flight time is most critical.

Non-coplanar Trajectories

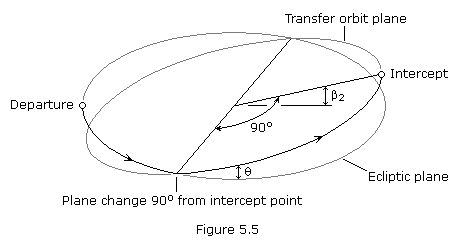
Up to now we have assumed that the planetary orbits all lie in the plane of the ecliptic. However, we know that all planets other than Earth have orbits inclined to the ecliptic. A good procedure to use when the target planet lies above or below the ecliptic at intercept is to launch the spacecraft into a transfer orbit that lies in the ecliptic plane and then make a simple plane change during mid-course when the true anomaly change remaining to intercept is 90-degrees. This minimizes the magnitude of the plane change required and is illustrated in Figure 5.4 below. Since the plane change is made 90^o short of intercept, the required inclination is just equal to the ecliptic latitude, , of the target planet at the time of intercept, t₂. The V required to produce a plane change was examined previously, and is calculated using equation (4.73).

 

Alternatively, the injection maneuver that places the spacecraft on its interplanetary trajectory can include a plane change to correctly orient the plane of the transfer orbit to intercept the target planet. Such an orbit between Earth and Mars is pictured in Figure 5.6 below. Since Earth lies in the ecliptic plane, the departure point defines one of the transfer orbit’s two nodes, with the other node 180 degrees away on the opposite side of the Sun. Unless the target planet happens to also be passing through one of its nodes at the time of interception, a near 180-degree transfer is not possible without a prohibitively high inclination. Intercepting the target with a true anomaly change several degrees less than 180^o (as pictured) or several degrees more than 180^o can be achieved with a manageably low inclination.

 

PROBLEM 5.1 

Using a one-tangent burn, calculate the change in true anomaly and the
time-of-flight for a transfer from Earth to Mars.  The radius vector of Earth at
departure is 1.000 AU and that of Mars at arrival is 1.524 AU.  The semi-major
axis of the transfer orbit is 1.300 AU.

SOLUTION,

   Given:  rA = 1.000 AU
           rB = 1.524 AU
           atx = 1.300 AU × 149.597870×109 m/AU = 194.48×109 m

   From Basics Constants,

      GM of Sun = 1.327124×1020 m3/s2

   Equations (4.66) and (4.67),

      e = 1 - rA / atx
      e = 1 - 1.0 / 1.3
      e = 0.230769

       = arccos[(atx × (1 - e2) / rB - 1) / e ]  
       = arccos[(1.3 × (1 - 0.2307692) / 1.524 - 1) / 0.230769 ]
       = 146.488 degrees 

   Equations (4.70) and (4.71),

      E = arctan[(1 - e2)1/2 × sin  / (e + cos )]
      E = arctan[(1 - 0.2307692)1/2 × sin(146.488) / (0.230769 + cos(146.588))]
      E = 2.41383 radians 

      TOF = (E - e × sin E) × SQRT[ atx3 / GM ]
      TOF = (2.41383 - 0.230769 × sin(2.41383)) × SQRT[ (194.48×109)3 / 1.327124×1020 ] 
      TOF = 16,827,800 s = 194.77 days

---

PROBLEM 5.2 

For the transfer orbit in problem 5.1, calculate the departure phase angle, given
that the angular velocity of Mars is 0.5240 degrees/day.

SOLUTION,

   Given:  2-1 = 146.488o
           t2-t1 = 194.77 days
           t = 0.5240o/day

   Equation (5.1),

       = (2-1) - t × (t2-t1)
       = 146.488 - 0.5240 × 194.77
       = 44.43o

---