Interplanetary flight:
1) Introduction
2) Heliocentric Transfer Orbit
4) Determining Orbital Elements
5) Hyperbolic Departure and Approach
On New Year’s Day 1801, Giuseppe Piazzi of Italy observed for the first time an object that turned out to be the minor planet Ceres. He was only able to observe the asteroid for about one month before it was lost in the glare of the Sun. The challenge of rediscovering Ceres when it reappeared from behind the Sun seduced the intellect of young German mathematician Carl Friedrich Gauss. Exactly one year later, on New Year’s Day 1802, Ceres was rediscovered precisely where the ingenious and detailed calculations of Gauss had predicted she must be found.
The method that Gauss used is just as pertinent today as it was in 1802, but for a different reason. The data that Gauss used to determine the orbit of Ceres consisted of the right ascension and declination at three observation times. His method is much simplified if the original data consists to two position vectors and the time-of-flight between them. The technique of determining an orbit from two position vectors and time is of considerable interest to modern astrodynamics since it has direct application in the solution of intercept and rendezvous. We may define the Gauss problem as follows: Given position vectors r1 and r2, the time of flight from r1 to r2, which we will call t, and the direction of motion, find velocity vectors v1 andv2. By “direction of motion” we mean whether the satellite is to go from r1 to r2 the “short way”, through an angular change (![]()
![]() ) of less than
) of less than ![]() radians, or the “long way”, through an angular change greater than
radians, or the “long way”, through an angular change greater than ![]() radians. Obviously, there are an infinite number of orbits passing through r1 and r2, but only two that have the specified time-of-flight – one for each possible direction of motion.
radians. Obviously, there are an infinite number of orbits passing through r1 and r2, but only two that have the specified time-of-flight – one for each possible direction of motion.
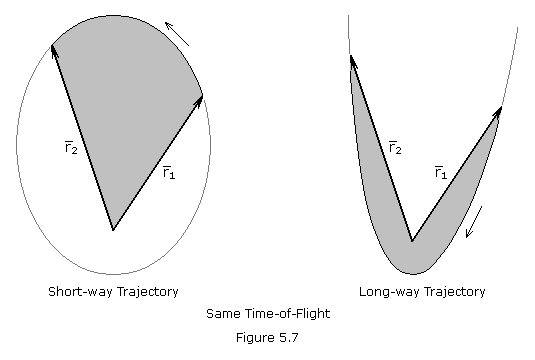
One thing is immediately obvious from Figure 5.7; the two vectors r1 and r2 uniquely define the plane of the transfer orbit. If the vectors r1 and r2 are collinear and in opposite directions (![]()
![]() =
=![]() ), the plane of the transfer orbit is not determined and a unique solution for v1 and v2 is not possible. If the two position vectors are collinear and in the same direction (
), the plane of the transfer orbit is not determined and a unique solution for v1 and v2 is not possible. If the two position vectors are collinear and in the same direction (![]()
![]() =0 or 2
=0 or 2![]() ), the orbit is a degenerate conic, but a unique solution is possible of v1 and v2. The relationship between the four vectors r1, r2, v1 and v2 is contained in the f and g expressions given below. It is not surprising, therefore, that nearly every known method for solving the Gauss problem may be derived from the f and g relations.
), the orbit is a degenerate conic, but a unique solution is possible of v1 and v2. The relationship between the four vectors r1, r2, v1 and v2 is contained in the f and g expressions given below. It is not surprising, therefore, that nearly every known method for solving the Gauss problem may be derived from the f and g relations.
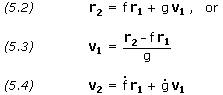
where,
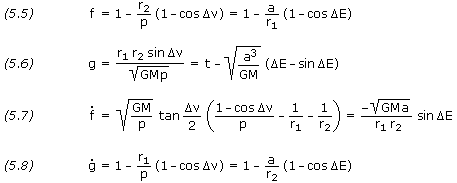
As previously defined, ![]() is true anomaly, E is eccentric anomaly, a is semi-major axis, and GM is the standard gravitational parameter, while p is a geometrical constant of the conic section called the parameter or semi-latus rectum.
is true anomaly, E is eccentric anomaly, a is semi-major axis, and GM is the standard gravitational parameter, while p is a geometrical constant of the conic section called the parameter or semi-latus rectum.
Consider equations (5.5), (5.6) and (5.7). There are seven variables — r1, r2, ![]()
![]() , t, p, a and
, t, p, a and ![]() E — but the first four are known, so what we have is three equations in three unknowns. The only trouble is that the equations are transcendental in nature, so a trial-and-error solution is necessary. We may outline the general method of solution as follows:
E — but the first four are known, so what we have is three equations in three unknowns. The only trouble is that the equations are transcendental in nature, so a trial-and-error solution is necessary. We may outline the general method of solution as follows:
- Guess a trial value for one of the three unknowns, p, a or
 E directly or indirectly by guessing some other parameter of the transfer orbit that in turn establishes p, a or
E directly or indirectly by guessing some other parameter of the transfer orbit that in turn establishes p, a or  E.
E. - Use equations (5.5) and (5.7) to compute the remaining two unknowns.
- Test the result by solving equation (5.6) for t and check it against the given value of time-of-flight.
- If the computed value of t does not agree with the given value, adjust the trial value of the iteration variable and repeat the procedure until it does agree.
The last step is perhaps the most important of all, since the method used to adjust the trial value of the iteration variable is what determines how quickly the procedure converges to a solution. There are several methods for solving the Gauss problem, however the only one we will present here is the p-iteration technique. The method consists of guessing a trial value of pfrom which we can compute a and ![]() E. The first step in the solution is to find an expression for a as a function of p and the given information. We will find it convenient to define three constants that may be determined from the given information:
E. The first step in the solution is to find an expression for a as a function of p and the given information. We will find it convenient to define three constants that may be determined from the given information:
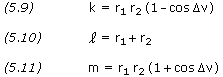
where r1 = |r1| and r2 = |r2|.
Once p is specified, a unique value of a is determined from
![]()
Once we have selected a trial value of p and computed a from equation (5.12), we are ready to solve for t and check it against the given time-of-flight. First, however, we need to determine ![]() E, or
E, or ![]() F in case a is negative (i.e. the orbit is hyperbolic).
F in case a is negative (i.e. the orbit is hyperbolic).
From the trail value of p and the known information, we can compute f, g and ![]() from equations (5.5), (5.6) and (5.7). If a is positive, we can determine
from equations (5.5), (5.6) and (5.7). If a is positive, we can determine ![]() E from equations (5.5) and (5.7), rearranged as follows:
E from equations (5.5) and (5.7), rearranged as follows:
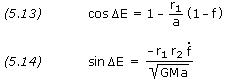
If a is negative, the corresponding f and g expressions involving ![]() F yield the following. Since we always assume
F yield the following. Since we always assume ![]() F is positive, there is no ambiguity in determining
F is positive, there is no ambiguity in determining ![]() F from this one equation.
F from this one equation.
![]()
The time-of-flight may now be determined from equation (5.16) or the corresponding equation involving ![]() F:
F:
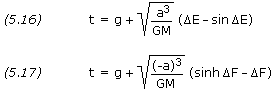
The limiting values of p correspond to two parabolic orbits passing through r1 and r2. The values of p that specify the parabolic orbits we’ll call pi and pii. For ![]()
![]() less than
less than ![]() radians, p must lie between pi and infinity. For
radians, p must lie between pi and infinity. For ![]()
![]() greater than
greater than ![]() radians, p must lie between 0 and pii. Since it is important that the first trial value, as well as all subsequent guesses for p, lie within the prescribed limits, we should first compute pi or pii.
radians, p must lie between 0 and pii. Since it is important that the first trial value, as well as all subsequent guesses for p, lie within the prescribed limits, we should first compute pi or pii.
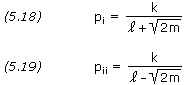
The method used to adjust the trial value of p to give the desired time-of-flight is crucial in determining how rapidly p converges to a solution. Several simple methods may be used successfully, such as the bisection or linear interpolation techniques.
In the bisection method we must find two trial values of p, one that gives too small a value for t and one that gives too large a value. The solution is then bracketed and, by choosing our next trial value half way between the first two, we can keep it bracketed while reducing the interval of uncertainty to some arbitrarily small value.
In the linear interpolation method we choose two trial values of p, which we will call pn-1 and pn. If tn-1 and tn are the times-of-flight corresponding to these trial values of p, then we select a new value from,
![]()
This scheme can be repeated, always retaining the latest two trial values of p and their corresponding times-of-flight for use in computing a still better trial value from equation (5.20). It is not necessary that the initial two trial values bracket the answer.
We can summarize the steps involved in solving the Gauss problem via the p-iteration technique as follows:
- Evaluate the constants k,
 and m from r1, r2 and
and m from r1, r2 and 
 using equations (5.9) through (5.11).
using equations (5.9) through (5.11). - Determine the limits on the possible values of p by evaluating pi and pii from equations (5.18) and (5.19).
- Pick a trial value of p within the appropriate limits.
- Using the trial value of p, solve for a from equation (5.12). The type conic orbit will be known from the value of a.
- Solve for f, g and
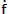 from equations (5.5), (5.6) and (5.7).
from equations (5.5), (5.6) and (5.7). - Solve for
 E or
E or  F, as appropriate, using equations (5.13) and (5.14) or equation (5.15).
F, as appropriate, using equations (5.13) and (5.14) or equation (5.15). - Solve for t from equation (5.16) or (5.17) and compare it with the desired time-of-flight.
- Adjust the trial value of p using one of the iteration methods discussed above until the desired time-of-flight is obtained.
- Evaluate
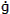 from equation (5.8) and then solve for v1 and v2 using equations (5.3) and (5.4).
from equation (5.8) and then solve for v1 and v2 using equations (5.3) and (5.4).
The p-iteration method converges in all cases except when r1 and r2 are collinear. Its main disadvantage is that separate equations are used for the ellipse and hyperbola.
Selecting a Transfer Orbit
Each time the Gauss problem is solved, the result gives just one of an infinite number of possible transfer orbits. It was previously stated that is generally desirable that the transfer orbit be tangential to Earth’s orbit at departure. This is true only in that it minimizes the ![]() V required to inject the spacecraft into its transfer orbit; however, it likely results in a less than optimum condition at target intercept. A one-tangent burn produces a trajectory that crosses the orbit of the target planet with a relatively large flight path angle, resulting in a large relative velocity between the spacecraft and planet. This relative velocity can be significantly reduced by selecting a transfer orbit that reduces the angle between the velocity vectors of the spacecraft and target at the moment of intercept. Improving the intercept condition (1) increases the duration of a close flyby encounter, (2) reduces the
V required to inject the spacecraft into its transfer orbit; however, it likely results in a less than optimum condition at target intercept. A one-tangent burn produces a trajectory that crosses the orbit of the target planet with a relatively large flight path angle, resulting in a large relative velocity between the spacecraft and planet. This relative velocity can be significantly reduced by selecting a transfer orbit that reduces the angle between the velocity vectors of the spacecraft and target at the moment of intercept. Improving the intercept condition (1) increases the duration of a close flyby encounter, (2) reduces the ![]() V required for orbit insertion, or (3) lowers the spacecraft’s velocity at atmospheric entry.
V required for orbit insertion, or (3) lowers the spacecraft’s velocity at atmospheric entry.
Tables 2 and 3 below provide sample data for a hypothetical mission to Mars in the year 2020. Table 2 gives the ![]() V required for Trans-Mars Injection (TMI) for a variety of different departure dates and times of flight. TMI is the maneuver that places the spacecraft into a trajectory that will intercept Mars at the desired place and time. In this sample, it is assumed that TMI is performed from an Earth parking orbit with an altitude of 200 km. Table 3 gives the
V required for Trans-Mars Injection (TMI) for a variety of different departure dates and times of flight. TMI is the maneuver that places the spacecraft into a trajectory that will intercept Mars at the desired place and time. In this sample, it is assumed that TMI is performed from an Earth parking orbit with an altitude of 200 km. Table 3 gives the ![]() V required for Mars-Orbit Insertion (MOI) for the same departure dates and times of flight found in Table 2. MOI, as it names implies, is the maneuver that slows the spacecraft to a velocity that places it into the desired orbit around Mars. In this sample, it is assumed that MOI is performed at periapsis of a insertion orbit with a periapsis altitude of 1,000 km and an apoapsis altitude of 33,000 km. Placing a spacecraft into a high eccentricity orbit such as this is common, as it provides for a MOI burn with a relatively low
V required for Mars-Orbit Insertion (MOI) for the same departure dates and times of flight found in Table 2. MOI, as it names implies, is the maneuver that slows the spacecraft to a velocity that places it into the desired orbit around Mars. In this sample, it is assumed that MOI is performed at periapsis of a insertion orbit with a periapsis altitude of 1,000 km and an apoapsis altitude of 33,000 km. Placing a spacecraft into a high eccentricity orbit such as this is common, as it provides for a MOI burn with a relatively low ![]() V.
V.
| Table 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Trans-Mars Injection DV (m/s), launch altitude = 200 km | |||||||||||
| Departure Date, 2020 |
Time of Flight (days) | ||||||||||
| 180 | 185 | 190 | 195 | 200 | 205 | 210 | 215 | 220 | 225 | 230 | |
| 7/7 | 3876 | 3862 | 3854 | 3851 | 3853 | 3863 | 3881 | 3912 | 3962 | 4043 | 4180 |
| 7/12 | 3841 | 3830 | 3824 | 3823 | 3826 | 3835 | 3851 | 3877 | 3917 | 3978 | 4074 |
| 7/19 | 3819 | 3812 | 3808 | 3808 | 3811 | 3819 | 3833 | 3853 | 3882 | 3925 | 3988 |
| 7/26 | 3834 | 3829 | 3826 | 3826 | 3829 | 3836 | 3846 | 3862 | 3883 | 3913 | 3956 |
| 8/2 | 3892 | 3887 | 3885 | 3884 | 3886 | 3890 | 3897 | 3908 | 3923 | 3943 | 3972 |
| 8/9 | 3999 | 3994 | 3990 | 3987 | 3987 | 3987 | 3991 | 3996 | 4005 | 4017 | 4034 |
| 8/16 | 4162 | 4154 | 4147 | 4141 | 4137 | 4133 | 4131 | 4131 | 4133 | 4138 | 4146 |
| 8/23 | 4386 | 4373 | 4362 | 4351 | 4341 | 4332 | 4325 | 4318 | 4313 | 4310 | 4309 |
| Table 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mars Orbit Insertion DV (m/s), insertion orbit = 1000 × 33000 km | |||||||||||
| Departure Date, 2020 |
Time of Flight (days) | ||||||||||
| 180 | 185 | 190 | 195 | 200 | 205 | 210 | 215 | 220 | 225 | 230 | |
| 7/7 | 1371 | 1258 | 1163 | 1086 | 1025 | 982 | 959 | 957 | 984 | 1052 | 1187 |
| 7/12 | 1290 | 1188 | 1102 | 1033 | 979 | 940 | 918 | 915 | 933 | 982 | 1074 |
| 7/19 | 1186 | 1097 | 1024 | 965 | 920 | 888 | 870 | 866 | 879 | 911 | 970 |
| 7/26 | 1093 | 1019 | 957 | 909 | 872 | 847 | 833 | 830 | 840 | 864 | 905 |
| 8/2 | 1016 | 954 | 904 | 865 | 837 | 818 | 808 | 808 | 817 | 836 | 867 |
| 8/9 | 957 | 907 | 868 | 838 | 817 | 804 | 799 | 801 | 811 | 828 | 853 |
| 8/16 | 920 | 881 | 852 | 830 | 816 | 809 | 808 | 813 | 823 | 839 | 862 |
| 8/23 | 910 | 881 | 860 | 846 | 838 | 836 | 839 | 846 | 857 | 873 | 893 |
- Calculate
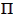 and
and 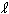 o,
o,
![]() (
(![]() and
and ![]() o are always less than 360o)
o are always less than 360o)
The angle ![]() , longitude of periapsis, is sometimes used in place of argument of periapsis. As a substitute for the time of periapsis passage, any of the following may be used to locate the spacecraft at a particular time, to, known as the “epoch”:
, longitude of periapsis, is sometimes used in place of argument of periapsis. As a substitute for the time of periapsis passage, any of the following may be used to locate the spacecraft at a particular time, to, known as the “epoch”: ![]() o, true anomaly at epoch, uo, argument of latitude at epoch, or
o, true anomaly at epoch, uo, argument of latitude at epoch, or ![]() o, true longitude at epoch.
o, true longitude at epoch.
If there is no periapsis (circular orbit), then ![]() is undefined, and
is undefined, and ![]() o =
o = ![]() + uo. If there is no ascending node (equatorial orbit), then both
+ uo. If there is no ascending node (equatorial orbit), then both ![]() and uo are undefined, and
and uo are undefined, and ![]() o =
o = ![]() +
+ ![]() o. If the orbit is both circular and equatorial,
o. If the orbit is both circular and equatorial, ![]() o is simply the true angle from x to ro, both of which are always defined.
o is simply the true angle from x to ro, both of which are always defined.
The procedure outlined above describes a spacecraft in a solar orbit, but the method works equally well for satellites in Earth orbit, or around another planet or moon, where the position and velocity vectors are known in the geocentric-equatorial reference plane. Note, however, that it is customary for the geocentric-equatorial coordinate system to use unit vectors i, j and kinstead of x, y and z as used in the heliocentric-ecliptic system.
PROBLEM 5.3 A flight to Mars is launched on 2020-7-20, 0:00 UT. The planned time of flight is 207 days. Earth's postion vector at departure is 0.473265X - 0.899215Y AU. Mars' postion vector at intercept is 0.066842X + 1.561256Y + 0.030948Z AU. Calculate the parameter and semi-major axis of the transfer orbit. SOLUTION, Given: t = 207 days r1 = 0.473265X - 0.899215Y AU r2 = 0.066842X + 1.561256Y + 0.030948Z AU GM = 1.327124×1020 m3/s2 = 1.327124×1020 / (149.597870×109)3 = 3.964016×10-14 AU3/s2 From vector magnitude, r1 = SQRT[ 0.4732652 + (-0.899215)2 ] r1 = 1.016153 AU r2 = SQRT[ 0.0668422 + 1.5612562 + 0.0309482 ] r2 = 1.562993 AU From vector dot product,= arccos[ (0.473265 × 0.066842 - 0.899215 × 1.561256) / (1.016153 × 1.562993) ]
= 149.770967o Equations (5.9), (5.10) and (5.11), k = r1 × r2 × (1 - cos
) k = 1.016153 × 1.562993 × (1 - cos(149.770967)) k = 2.960511 AU
= r1 + r2
= 1.016153 + 1.562993
= 2.579146 AU m = r1 × r2 × (1 + cos
) m = 1.016153 × 1.562993 × (1 + cos(149.770967)) m = 0.215969 AU Equations (5.18) and (5.19), pi = k / (
+ SQRT(2 × m)) pi = 2.960511 / (2.579146 + SQRT(2 × 0.215969)) pi = 0.914764 AU pii = k / (
- SQRT(2 × m)) pii = 2.960511 / (2.579146 - SQRT(2 × 0.215969)) pii = 1.540388 AU Since
<
, 0.914764 < p <
Equation (5.12), Select trial value, p = 1.2 AU a = m × k × p / [(2 × m -
2) × p2 + 2 × k ×
× p - k2] a = 0.215969 × 2.960511 × 1.2 / [(2 × 0.215969 - 2.5791462) × 1.22 + 2 × 2.960511 × 2.579146 × 1.2 - 2.9605112] a = 1.270478 AU Equations (5.5), (5.6) and (5.7), f = 1 - r2 / p × (1 - cos
) f = 1 - 1.562993 / 1.2 × (1 - cos(149.770967)) f = -1.427875 g = r1 × r2 × sin
/ SQRT[ GM × p ] g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.2 ] g = 3,666,240
= SQRT[ GM / p ] × tan(
/2) × [(1 - cos
) / p - 1/r1 - 1/r2 ]
= SQRT[ 3.964016×10-14 / 1.2 ] × tan(149.770967/2) × [(1 - cos(149.770967)) / 1.2 - 1/1.016153 - 1/1.562993 ]
= -4.747601×10-8 Equation (5.13),
E = arccos[ 1 - r1 / a × (1 - f) ]
E = arccos[ 1 - 1.016153 / 1.270478 × (1 + 1.427875) ]
E = 2.798925 radians Equation (5.16), t = g + SQRT[ a3 / GM ] × (
E - sin
E) t = 3,666,240 + SQRT[ 1.2704783 / 3.964016×10-14 ] × (2.798925 - sin(2.798925)) t = 21,380,951 s = 247.4647 days Select new trial value of p and repeat above steps, p = 1.300000 AU, a = 1.443005 AU, t = 178.9588 days Equation (5.20), pn+1 = pn + (t - tn) × (pn - pn-1) / (tn - tn-1) pn+1 = 1.3 + (207 - 178.9588) × (1.3 - 1.2) / (178.9588 - 247.4647) pn+1 = 1.259067 AU Recalculate using new value of p, p = 1.259067 AU, a = 1.336197 AU, t = 201.5624 days Perform additional iterations, p = 1.249221 AU, a = 1.318624 AU, t = 207.9408 days p = 1.250673 AU, a = 1.321039 AU, t = 206.9733 days p = 1.250633 AU, a = 1.320971 AU, t = 206.9999 days <-- close enough
PROBLEM 5.4 For the Mars transfer orbit in Problem 5.3, calculate the departure and intecept velocity vectors. SOLUTION, Given: r1 = 0.473265X - 0.899215Y AU r2 = 0.066842X + 1.561256Y + 0.030948Z AU r1 = 1.016153 AU r2 = 1.562993 AU p = 1.250633 AU a = 1.320971 AU= 149.770967o Equations (5.5), (5.6) and (5.7), f = 1 - r2 / p × (1 - cos
) f = 1 - 1.562993 / 1.250633 × (1 - cos(149.770967)) f = -1.329580 g = r1 × r2 × sin
/ SQRT[ GM × p ] g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.250633 ] g = 3,591,258
= SQRT[ GM / p ] × tan(
/2) × [(1 - cos
) / p - 1/r1 - 1/r2 ]
= SQRT[ 3.964016×10-14 / 1.250633 ] × tan(149.770967/2) × [(1 - cos(149.770967)) / 1.250633 - 1/1.016153 - 1/1.562993 ]
= -8.795872×10-8
= 1 - r1 / p × (1 - cos
)
= 1 - 1.016153 / 1.250633 × (1 - cos(149.770967))
= -0.514536 Equation (5.3), v1 = (r2 - f × r1) / g v1 = [(0.066842 + 1.329580 × 0.473265) / 3,591,258] X + [(1.561256 + 1.329580 × -0.899215) / 3,591,258] Y + [(0.030948 + 1.329580 × 0) / 3,591,258] Z v1 = 0.000000193828X + 0.000000101824Y + 0.00000000861759Z AU/s × 149.597870×109 v1 = 28996.2X + 15232.7Y + 1289.2Z m/s Equation (5.4), v2 =
× r1 +
× v1 v2 = [-8.795872×10-8 × 0.473265 - 0.514536 × 0.000000193828] X + [-8.795872×10-8 × -0.899215 - 0.514536 × 0.000000101824] Y + [-8.795872×10-8 × 0 - 0.514536 × 0.00000000861759] Z v2 = -0.000000141359X + 0.0000000267017Y - 0.00000000443406Z AU/s × 149.597870×109 v2 = -21147.0X + 3994.5Y - 663.3Z m/s
PROBLEM 5.5 For the Mars transfer orbit in Problems 5.3 and 5.4, calculate the orbital elements. SOLUTION, Problem can be solved using either r1 & v1 or r2 & v2 – we will use r1 & v1. Given: r1 = (0.473265X - 0.899215Y AU) × 149.597870×109 m/AU = 7.079944×1010X - 1.345206×1011Y m r1 = 1.016153 × 149.597870×109 = 1.520144×1011 m GM = 1.327124×1020 m3/s2 From problem 5.4, v1 = 28996.2X + 15232.7Y + 1289.2Z m/s Also, v = SQRT[ 28996.22 + 15232.72 + 1289.22 ] = 32,779.2 m/s Equations (5.21) and (5.22), h = (rY vZ - rZ vY)X + (rZ vX - rX vZ)Y + (rX vY - rY vX)Z h = (-1.345206×1011 × 1289.2 - 0 × 15232.7)X + (0 × 28996.2 - 7.079944×1010 × 1289.2)Y + (7.079944×1010 × 15232.7 + 1.345206×1011 × 28996.2)Z h = -1.73424×1014X - 9.12746×1013Y + 4.97905×1015Z n = -hY X + hX Y n = 9.12746×1013X - 1.73424×1014Y Also, h = SQRT[ (-1.73424×1014)2 + (-9.12746×1013)2 + (4.97905×1015)2 ] = 4.98291×1015 n = SQRT[ (9.12746×1013)2 + (1.73424×1014)2 ] = 1.95977×1014 Equation (5.23), e = [(v2 - GM / r) × r - (r • v) × v ] / GM v2 - GM / r = 32779.22 - 1.327124×1020 / 1.520144×1011 = 2.01451×108 r • v = 7.079944×1010 × 28996.2 - 1.345206×1011 × 15232.7 + 0 x 1289.2 = 3.80278×1012 e = [2.01451×108 × (7.079944×1010X - 1.345206×1011Y) - 3.80278×1012 × (28996.2X + 15232.7Y + 1289.2Z) ] / 1.327124×1020 e = 0.106639X - 0.204632Y - 0.000037Z Equations (5.24) and (5.25), a = 1 / ( 2 / r - v2 / GM ) a = 1 / ( 2 / 1.520144×1011 - 32779.22 / 1.327124×1020 ) a = 1.97614×1011 m e = SQRT[ 0.1066392 + (-0.204632)2 + (-0.000037)2 ] e = 0.230751 Equations (5.26) though (5.30), cos i = hZ / h cos i = 4.97905×1015 / 4.98291×1015 i = 2.255o cos= nX / n cos
= 9.12746×1013 / 1.95977×1014
= 297.76o cos
= n • e / (n × e) cos
= (9.12746×1013 × 0.106639 - 1.73424×1014 × (-0.204632) + 0 × (-0.000037)) / (1.95977×1014 × 0.230751)
= 359.77o cos
o = e • r / (e × r) cos
o = (0.106639 × 7.079944×1010 - 0.204632 × (-1.345206×1011) - 0.000037 × 0) / (0.230751 × 1.520144×1011)
o = 0.226o cos uo = n • r / (n × r) uo = 0 (launch point = ascending node) Equations (5.31) and (5.32),
=
+
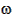
= 297.76 + 359.77
= 297.53o
o =
+
+
o
o = 297.76 + 359.77 + 0.23
o = 297.76o