Interplanetary flight:
1) Introduction
2) Heliocentric Transfer Orbit
4) Determining Orbital Elements
5) Hyperbolic Departure and Approach
In planning certain types of trajectories of spacecraft within the solar system, engineers rely on a technique called gravitational assist (also gravity assist, slingshot, or swing-by). This technique underlies the feasibility of effecting a net change in both the speed and direction of motion of a spacecraft by passage through the gravitational field of a planet or a planetary satellite, typically in order to save propellant, time, and expense.
A gravitational assist around a planet changes a spacecraft’s velocity relative to the Sun by entering and leaving the gravitational field of a planet. The spacecraft accelerates as it approaches the planet and decelerates while escaping its gravitational pull. Because the planet orbits the Sun, this motion affects the spacecraft during the maneuver. To accelerate, the spacecraft flies across the trailing side of the planet, taking a small amount of the planet’s orbital energy (as pictured in Figure 5.13). To decelerate, the spacecraft flies across the leading side of the planet. The sum of the kinetic energies of both bodies remains constant. A gravitational assist can therefore be used to change the spaceship’s trajectory and speed relative to the Sun.
The resulting increase, or decrease, in the kinetic energy of the spacecraft appears to contradict the casual expectation that in such an encounter the kinetic energy of the spacecraft after the encounter would be the same as that before the encounter. However, the energy gained by the spaceship is equal in magnitude to that lost by the planet, though the planet’s enormous mass compared to the spacecraft makes the resulting change in its speed negligibly small. These effects on the planet are so slight that they can be ignored in the calculation.
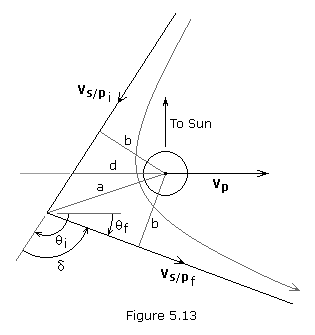
- Orbits of planet and spacecraft are coplanar.
- Y-axis is parallel to the planet’s position vector, positive outward from Sun.
- X-axis is in the orbital plane normal to the Y-axis, positive in the prograde direction.
- Planet’s velocity (Vp) and flight path angle (
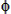 p) are given.
p) are given. - Spacecraft’s initial velocity (Vsi), flight path angle (
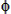 si), and miss distance (d) are given.
si), and miss distance (d) are given.
The planet’s velocity vector and the spacecraft’s initial velocity vector are solved for using,
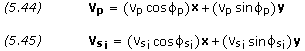
The initial relative velocity vector and its magnitude are solved for using,
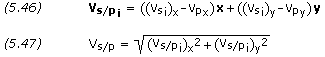
(Recall that V∞ ≈ Vs/p)
The angle ![]() i is obtained as follows (making sure to check quadrant),
i is obtained as follows (making sure to check quadrant),
![]()
The impact parameter, b, semi-major axis, a, and eccentricity, e, are solved for using equations (5.40), (5.41) and (5.42).
The turning angle, ![]() , is solved for using equation (4.80), and the angle
, is solved for using equation (4.80), and the angle ![]() f is calculated as follows,
f is calculated as follows,
![]()
The final relative velocity vector is,
![]()
And the spacecraft’s final velocity vector and magnitude are,
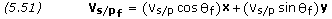
Finally, we calculate the spacecraft’s final flight path angle as follows,
![]()
PROBLEM 5.8
As a spacecraft approaches Jupiter, it has a velocity of 9,470 m/s, a flight
path angle of 39.2 degrees, and a targeted miss distance of -2,500,000 km. At
intercept, Jupiter's velocity is 12,740 m/s with a flight path angle of 2.40
degrees. Calculate the spacecraft's velocity and flight path angle following
its swing-by of Jupiter.
Given: VP = 12,740 m/s
 P = 2.40o
VSi = 9,470 m/s
P = 2.40o
VSi = 9,470 m/s
 Si = 39.2o
d = -2,500,000 km
From Basics Constants,
GM of Jupiter = 1.26686×1017 m3/s2
Equations (5.44) and (5.45),
VP = (VP × cos
Si = 39.2o
d = -2,500,000 km
From Basics Constants,
GM of Jupiter = 1.26686×1017 m3/s2
Equations (5.44) and (5.45),
VP = (VP × cos 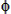 P)X + (VP × sin
P)X + (VP × sin 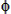 P)Y
VSi = (12740 × cos(2.40))X + (12740 × sin(2.40))Y
VSi = 12729X + 533Y m/s
VSi = (VSi × cos
P)Y
VSi = (12740 × cos(2.40))X + (12740 × sin(2.40))Y
VSi = 12729X + 533Y m/s
VSi = (VSi × cos 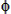 Si)X + (VSi × sin
Si)X + (VSi × sin 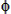 Si)Y
VSi = (9470 × cos(39.2))X + (9470 × sin(39.2))Y
VSi = 7339X + 5985Y m/s
Equations (5.46) and (5.47),
VS/Pi = ((VSi)X – VPX)X + ((VSi)Y – VPY)Y
VS/Pi = (7339 – 12729)X + (5985 – 533)Y
VS/Pi = –5390X + 5452Y m/s
VS/P = SQRT[ (VS/Pi)X2 + (VS/Pi)Y2 ]
VS/P = SQRT[ (-5390)2 + 54522 ]
VS/P = 7,667 m/s
V
Si)Y
VSi = (9470 × cos(39.2))X + (9470 × sin(39.2))Y
VSi = 7339X + 5985Y m/s
Equations (5.46) and (5.47),
VS/Pi = ((VSi)X – VPX)X + ((VSi)Y – VPY)Y
VS/Pi = (7339 – 12729)X + (5985 – 533)Y
VS/Pi = –5390X + 5452Y m/s
VS/P = SQRT[ (VS/Pi)X2 + (VS/Pi)Y2 ]
VS/P = SQRT[ (-5390)2 + 54522 ]
VS/P = 7,667 m/s
V = VS/P = 7,667 m/s
Equation (5.48),
= VS/P = 7,667 m/s
Equation (5.48),
 i = arctan[ (VS/Pi)Y / (VS/Pi)X ]
i = arctan[ (VS/Pi)Y / (VS/Pi)X ]
 i = arctan[ 5452 / -5390 ]
i = arctan[ 5452 / -5390 ]
 i = 134.67o
Equations (5.40) through (5.42),
b = d × sin
i = 134.67o
Equations (5.40) through (5.42),
b = d × sin  b = -2,500,000 × sin(134.67)
b = -1,777,900 km
a = -GM / V
b = -2,500,000 × sin(134.67)
b = -1,777,900 km
a = -GM / V 2
a = -1.26686×1017 / 76672
a = -2.1552×109 m = -2,155,200 km
e = SQRT[ 1 + b2 / a2 ]
e = SQRT[ 1 + (-1,777,900)2 / (-2,155,200)2 ]
e = 1.2963
Equation (4.80),
sin(
2
a = -1.26686×1017 / 76672
a = -2.1552×109 m = -2,155,200 km
e = SQRT[ 1 + b2 / a2 ]
e = SQRT[ 1 + (-1,777,900)2 / (-2,155,200)2 ]
e = 1.2963
Equation (4.80),
sin(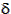 /2) = 1 / e
/2) = 1 / e
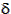 = 2 × arcsin( 1 / 1.2963 )
= 2 × arcsin( 1 / 1.2963 )
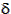 = 100.96o
Equation (5.49),
= 100.96o
Equation (5.49),
 f =
f =  i –
i – 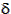
 f = 134.67 - 100.96
f = 134.67 - 100.96
 f = 33.71o
Equation (5.50),
VS/Pf = (VS/P × cos
f = 33.71o
Equation (5.50),
VS/Pf = (VS/P × cos  f)X + (VS/P × sin
f)X + (VS/P × sin  f)Y
VS/Pf = (7667 × cos(33.71))X + (7667 × sin(33.71))Y
VS/Pf = 6378X + 4255Y m/s
Equations (5.51) and (5.52),
VSf = ((VS/Pf)X + VPX)X + ((VS/Pf)Y + VPY)Y
VSf = (6378 + 12729)X + (4255 + 533)Y
VSf = 19107X + 4788Y m/s
VSf = SQRT[ (VSf)X2 + (VSf)Y2 ]
VSf = SQRT[ 191072 + 47882 ]
VSf = 19,698 m/s
Equation (5.53),
f)Y
VS/Pf = (7667 × cos(33.71))X + (7667 × sin(33.71))Y
VS/Pf = 6378X + 4255Y m/s
Equations (5.51) and (5.52),
VSf = ((VS/Pf)X + VPX)X + ((VS/Pf)Y + VPY)Y
VSf = (6378 + 12729)X + (4255 + 533)Y
VSf = 19107X + 4788Y m/s
VSf = SQRT[ (VSf)X2 + (VSf)Y2 ]
VSf = SQRT[ 191072 + 47882 ]
VSf = 19,698 m/s
Equation (5.53),
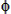 Sf = arctan[ (VSf)Y / (VSf)X ]
Sf = arctan[ (VSf)Y / (VSf)X ]
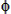 Sf = arctan[ 4788 / 19107 ]
Sf = arctan[ 4788 / 19107 ]
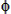 Sf = 14.07o
Sf = 14.07o