Rocket Propulsion:
– Thrust
– Combustion & Exhaust Velocity
– Staging
Solid rockets motors store propellants in solid form. The fuel is typically powdered aluminum and the oxidizer is ammonium perchlorate. A synthetic rubber binder such as polybutadiene holds the fuel and oxidizer powders together. Though lower performing than liquid propellant rockets, the operational simplicity of a solid rocket motor often makes it the propulsion system of choice.
Solid Fuel Geometry
A solid fuel’s geometry determines the area and contours of its exposed surfaces, and thus its burn pattern. There are two main types of solid fuel blocks used in the space industry. These are cylindrical blocks, with combustion at a front, or surface, and cylindrical blocks with internal combustion. In the first case, the front of the flame travels in layers from the nozzle end of the block towards the top of the casing. This so-called end burner produces constant thrust throughout the burn. In the second, more usual case, the combustion surface develops along the length of a central channel. Sometimes the channel has a star shaped, or other, geometry to moderate the growth of this surface.
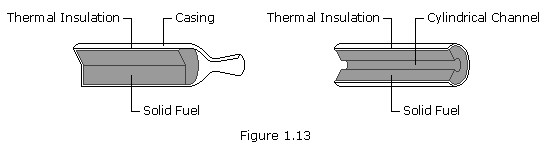
The shape of the fuel block for a rocket is chosen for the particular type of mission it will perform. Since the combustion of the block progresses from its free surface, as this surface grows, geometrical considerations determine whether the thrust increases, decreases or stays constant.
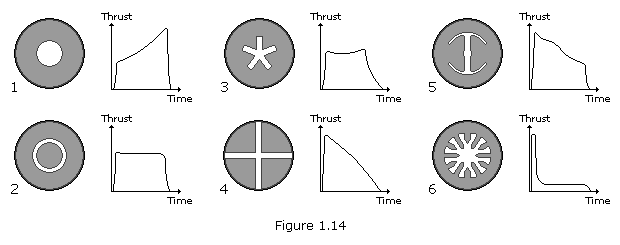
Fuel blocks with a cylindrical channel (1) develop their thrust progressively. Those with a channel and also a central cylinder of fuel (2) produce a relatively constant thrust, which reduces to zero very quickly when the fuel is used up. The five pointed star profile (3) develops a relatively constant thrust which decreases slowly to zero as the last of the fuel is consumed. The ‘cruciform’ profile (4) produces progressively less thrust. Fuel in a block with a ‘double anchor’ profile (5) produces a decreasing thrust which drops off quickly near the end of the burn. The ‘cog’ profile (6) produces a strong inital thrust, followed by an almost constant lower thrust.
Burn Rate
The burning surface of a rocket propellant grain recedes in a direction perpendicular to this burning surface. The rate of regression, typically measured in millimeters per second (or inches per second), is termed burn rate. This rate can differ significantly for different propellants, or for one particular propellant, depending on various operating conditions as well as formulation. Knowing quantitatively the burning rate of a propellant, and how it changes under various conditions, is of fundamental importance in the successful design of a solid rocket motor.
Propellant burning rate is influenced by certain factors, the most significant being: combustion chamber pressure, initial temperature of the propellant grain, velocity of the combustion gases flowing parallel to the burning surface, local static pressure, and motor acceleration and spin. These factors are discussed below.
- Burn rate is profoundly affected by chamber pressure. The usual representation of the pressure dependence on burn rate is the Saint-Robert’s Law,
 where r is the burn rate, a is the burn rate coefficient, n is the pressure exponent, and Pc is the combustion chamber pressure. The values of a and n are determined empirically for a particular propellant formulation and cannot be theoretically predicted. It is important to realize that a single set of a, n values are typically valid over a distinct pressure range. More than one set may be necessary to accurately represent the full pressure regime of interest.Example a, n values are 5.6059* (pressure in MPa, burn rate in mm/s) and 0.35 respectively for the Space Shuttle SRBs, which gives a burn rate of 9.34 mm/s at the average chamber pressure of 4.3 MPa.* NASA publications gives a burn rate coefficient of 0.0386625 (pressure in PSI, burn rate in inch/s).
where r is the burn rate, a is the burn rate coefficient, n is the pressure exponent, and Pc is the combustion chamber pressure. The values of a and n are determined empirically for a particular propellant formulation and cannot be theoretically predicted. It is important to realize that a single set of a, n values are typically valid over a distinct pressure range. More than one set may be necessary to accurately represent the full pressure regime of interest.Example a, n values are 5.6059* (pressure in MPa, burn rate in mm/s) and 0.35 respectively for the Space Shuttle SRBs, which gives a burn rate of 9.34 mm/s at the average chamber pressure of 4.3 MPa.* NASA publications gives a burn rate coefficient of 0.0386625 (pressure in PSI, burn rate in inch/s).
- Temperature affects the rate of chemical reactions and thus the initial temperature of the propellant grain influences burning rate. If a particular propellant shows significant sensitivity to initial grain temperature, operation at temperature extremes will affect the time-thrust profile of the motor. This is a factor to consider for winter launches, for example, when the grain temperature may be lower than “normal” launch conditions.
- For most propellants, certain levels of local combustion gas velocity (or mass flux) flowing parallel to the burning surface leads to an increased burning rate. This “augmentation” of burn rate is referred to as erosive burning, with the extent varying with propellant type and chamber pressure. For many propellants, a threshold flow velocity exists. Below this flow level, either no augmentation occurs, or a decrease in burn rate is experienced (negative erosive burning).The effects of erosive burning can be minimized by designing the motor with a sufficiently large port-to-throat area ratio (Aport/At). The port area is the cross-section area of the flow channel in a motor. For a hollow-cylindrical grain, this is the cross-section area of the core. As a rule of thumb, the ratio should be a minimum of 2 for a grain L/D ratio of 6. A greater Aport/At ratio should be used for grains with larger L/D ratios.
- In an operating rocket motor, there is a pressure drop along the axis of the combustion chamber, a drop that is physically necessary to accelerate the increasing mass flow of combustion products toward the nozzle. The static pressure is greatest where gas flow is zero, that is, at the front of the motor. Since burn rate is dependant upon the local pressure, the rate should be greatest at this location. However, this effect is relatively minor and is usually offset by the counter-effect of erosive burning.
- Burning rate is enhanced by acceleration of the motor. Whether the acceleration is a result of longitudinal force (e.g. thrust) or spin, burning surfaces that form an angle of about 60-90o with the acceleration vector are prone to increased burn rate.
It is sometimes desirable to modify the burning rate such that it is more suitable to a certain grain configuration. For example, if one wished to design an end burner grain, which has a relatively small burning area, it is necessary to have a fast burning propellant. In other circumstances, a reduced burning rate may be sought after. For example, a motor may have a large L/D ratio to generate sufficiently high thrust, or it may be necessary for a particular design to restrict the diameter of the motor. The web would be consequently thin, resulting in short burn duration. Reducing the burning rate would be beneficial.
There are a number of ways of modifying the burning rate: decrease the oxidizer particle size, increase or reduce the percentage of oxidizer, adding a burn rate catalyst or suppressant, and operate the motor at a lower or higher chamber pressure. These factors are discussed below.
- The effect of the oxidizer particle size on burn rate seems to be influenced by the type of oxidizer. Propellants that use ammonium perchlorate (AP) as the oxidizer have a burn rate that is significantly affected by AP particle size. This most likely results from the decomposition of AP being the rate-determining step in the combustion process.
- The burn rate of most propellants is strongly influenced by the oxidizer/fuel ratio. Unfortunately, modifying the burn rate by this means is quite restrictive, as the performance of the propellant, as well as mechanical properties, are also greatly affected by the O/F ratio.
- Certainly the best and most effective means of increasing the burn rate is the addition of a catalyst to the propellant mixture. A catalyst is a chemical compound that is added in small quantities for the sole purpose of tailoring the burning rate. A burn rate suppressant is an additive that has the opposite effect to that of a catalyst – it is used to decrease the burn rate.
- For a propellant that follows the Saint-Robert’s burn rate law, designing a rocket motor to operate at a lower chamber pressure will provide for a lower burning rate. Due to the nonlinearity of the pressure-burn rate relationship, it may be necessary to significantly reduce the operating pressure to get the desired burning rate. The obvious drawback is reduced motor performance, as specific impulse similarly decays with reducing chamber pressure.
Product Generation Rate
The rate at which combustion products are generated is expressed in terms of the regression speed of the grain. The product generation rate integrated over the port surface area is
![]()
where q is the combustion product generation rate at the propellant surface, ![]() p is the solid propellant density, Ab is the area of the burning surface, and r is the propellant burn rate. If the propellant density is unknown, it can be derived from the mass fraction and density of the individual constituents, as follows:
p is the solid propellant density, Ab is the area of the burning surface, and r is the propellant burn rate. If the propellant density is unknown, it can be derived from the mass fraction and density of the individual constituents, as follows:
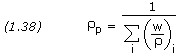
where w is the mass fraction and the subscript i denotes the individual constituents. This is the ideal density; the actual density is typically 94%-97% of the ideal density, owing to tiny voids in the grain, and is dependant upon the manufacturing technique.
Condensed-Phase Mass
It is important to note that the combustion products may consist of both gaseous and condensed-phase mass. The condensed-phase, which manifests itself as smoke, may be either solid or liquid particles. Only the gaseous products contribute to pressure development. The condensed-phase certainly does, however, contribute to the thrust of the rocket motor, due to its mass and velocity.
The occurrence of solids or liquids in a rocket’s exhaust leads to a reduction in performance for a number of reasons:
- This portion of the combustion mass cannot perform any expansion work and, therefore, does not contribute to acceleration of the exhaust flow.
- The higher effective molecular weight of these products lowers the characteristic exhaust velocity, C*.
- Due to thermal inertia, the heat of the condensed species is partly ejected out of the nozzle before transferring this heat to the surrounding gas, and is, therefore, not converted to kinetic energy. This is known asparticle thermal lag.
- Likewise, due to the relatively large mass of the particles (compared to the gases), these cannot accelerate as rapidly as the surrounding gases, especially in that portion of the nozzle where flow acceleration is extremely high (throat region). Acceleration of the particles depends upon frictional drag in the gas flow, which necessitates a differential velocity. The net result is that the condensed-phase particles exit the nozzle at a lower velocity than the gases. This is referred to as particle velocity lag.
Chamber Pressure
The pressure curve of a rocket motor exhibits transient and steady state behavior. The transient phases are when the pressure varies substantially with time – during the ignition and start-up phase, and following complete (or nearly complete) grain consumption when the pressure falls down to ambient level during the tail-off phase. The variation of chamber pressure during the steady state burning phase is due mainly to variation of grain geometry with associated burn rate variation. Other factors may play a role, however, such as nozzle throat erosion and erosive burn rate augmentation.
PROBLEM 1.10
A solid rocket motor burns along the face of a central cylindrical channel 10
meters long and 1 meter in diameter. The propellant has a burn rate coefficient
of 5.5, a pressure exponent of 0.4, and a density of 1.70 g/ml. Calculate the
burn rate and the product generation rate when the chamber pressure is 5.0 MPa.
SOLUTION,
Given: a = 5.5
n = 0.4
Pc = 5.0 MPa
 p = 1.70 g/ml
Ab =
p = 1.70 g/ml
Ab = 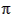 × 1 × 10 = 31.416 m2
Equation (1.36),
r = a × Pcn
r = 5.5 × 5.00.4 = 10.47 mm/s
Equation (1.37),
q =
× 1 × 10 = 31.416 m2
Equation (1.36),
r = a × Pcn
r = 5.5 × 5.00.4 = 10.47 mm/s
Equation (1.37),
q = 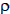 p × Ab × r
q = 1.70 × 31.416 × 10.47 = 559 kg/s
p × Ab × r
q = 1.70 × 31.416 × 10.47 = 559 kg/s
PROBLEM 1.11
Calculate the ideal density of a solid rocket propellant consisting of 68%
ammonium perchlorate, 18% aluminum, and 14% HTPB by mass.
SOLUTION,
Given: wAP = 0.68
wAl = 0.18
wHTPB = 0.14
From Properties of Rocket Propellants we have,
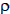 AP = 1.95 g/ml
AP = 1.95 g/ml
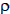 Al = 2.70 g/ml
Al = 2.70 g/ml
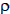 HTPB = ≈0.93 g/ml
Equation (1.38),
HTPB = ≈0.93 g/ml
Equation (1.38),
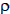 p = 1 /
p = 1 / 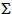 i (w /
i (w / 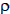 )i
)i
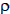 p = 1 / [(0.68 / 1.95) + (0.18 / 2.70) + (0.14 / 0.93)]
p = 1 / [(0.68 / 1.95) + (0.18 / 2.70) + (0.14 / 0.93)]
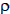 p = 1.767
p = 1.767