The rainflow ( “rain-flow counting method”) is used in the analysis of fatigue in order to reduce a spectrum of varying stress into a set of simple stress reversals. Its importance is that it allows the application of Miner’s rule in order to assess the fatigue life of a structure subject to complex loading.
procedure:
- Reduce the time history to a sequence of (tensile) peaks and (compressive) troughs.
- Imagine that the time history is a template for a rigid sheet (pagoda roof).
- Turn the sheet clockwise 90° (earliest time to the top).
- Each tensile peak is imagined as a source of water that “drips” down the pagoda.
- Count the number of half-cycles by looking for terminations in the flow occurring when either:
- It reaches the end of the time history;
- It merges with a flow that started at an earlier tensile peak; or
- It flows opposite a tensile peak of greater magnitude.
- Repeat step 5 for compressive troughs.
- Assign a magnitude to each half-cycle equal to the stress difference between its start and termination.
- Pair up half-cycles of identical magnitude (but opposite sense) to count the number of complete cycles. Typically, there are some residual half-cycles.
Example
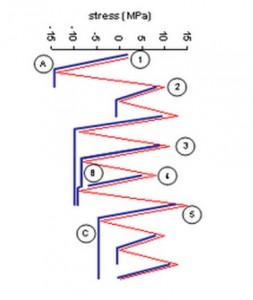
- The stress history in Figure 2 is reduced to peaks and troughs in Figure 3.
- Half-cycle (A) starts at tensile peak (1) and terminates opposite a greater tensile stress, peak (2). Its magnitude is 16 MPa.
- Half-cycle (B) starts at tensile peak (4) and terminates where it is interrupted by a flow from an earlier peak, (3), Its magnitude is 17 MPa.
- Half-cycle (C) starts at tensile peak (5) and terminates at the end of the time history.
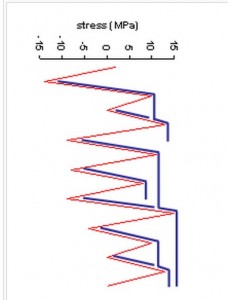
- Similar half-cycles are calculated for compressive stresses (Figure 4) and the half-cycles are then matched.
| Stress (MPa) | Whole cycles | Half cycles |
| 10 | 2 | 0 |
| 13 | 0 | 1 |
| 16 | 0 | 2 |
| 17 | 0 | 2 |
| 19 | 1 | 0 |
| 20 | 0 | 1 |
| 22 | 0 | 1 |
| 24 | 0 | 1 |
| 27 | 0 | 1 |
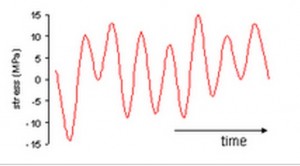
For simple periodic loadings, such as Figure 1, rainflow counting is unnecessary. In case the structure’s life can be estimated from a simple application of the relevant S-N curve.
if you have appreciated this post, please click on the banner below, thanks.