1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Matrix of Elasticity
1.4. Matrix of elasticity
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants
One the three matrices involved in the constitutive equation of a composite laminate are determining, the calculation of the deformations and of the tensions present on each ply can be calculated by using these equations in order to explicitate the variables of interest. According to the classical theory of laminated, deformations and tensions of each ply are connected with the deformation of components of the medium plane of the laminate. Therefore in calculation procedure of deformations and stresses is advantageous to evaluate the strain components in the middle plane and then to make an evaluation of variables locally for each lamina. The midplane strain components can in principle be calculated directly by the stress characteristics with reversing the equation (84) menthioned above. However, this involves the inversion of a 6×6 matrix, which can be avoided by means an alternative procedure that consist in to consider separately eq. (77) and (82):
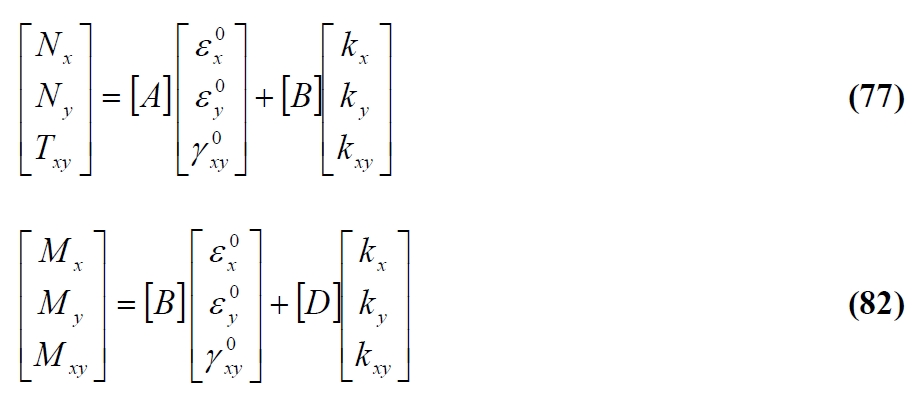
By solving the first with respect the deformations in the plane and the second with respect to the curvature, we have:
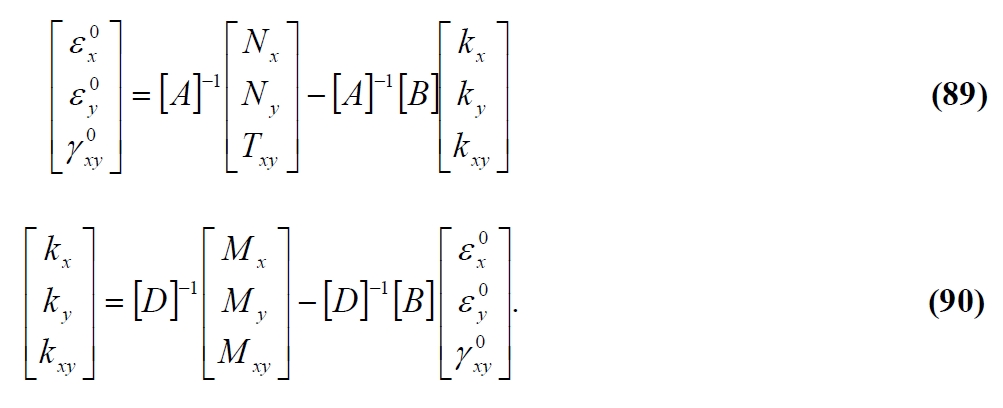
Then replacing the (89) in the (90) we have:
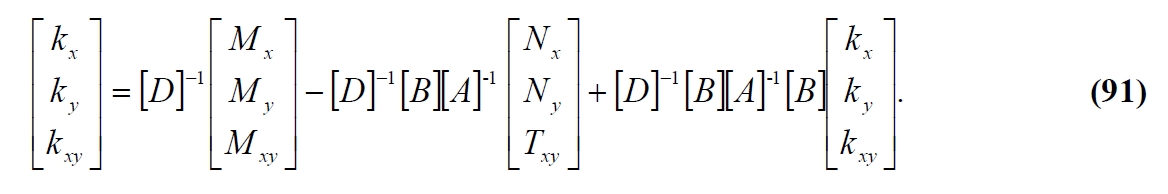
resolving the (91) with respect to curvatures and indicating with:

we have:
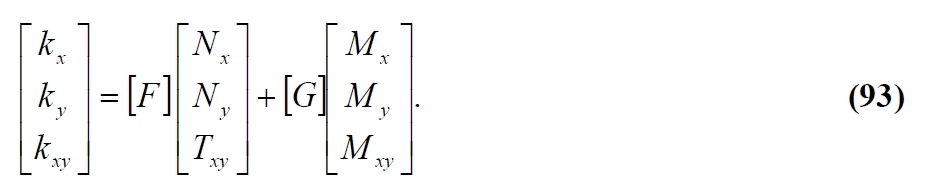
Then substituting the (93) in the (89) we obtain:
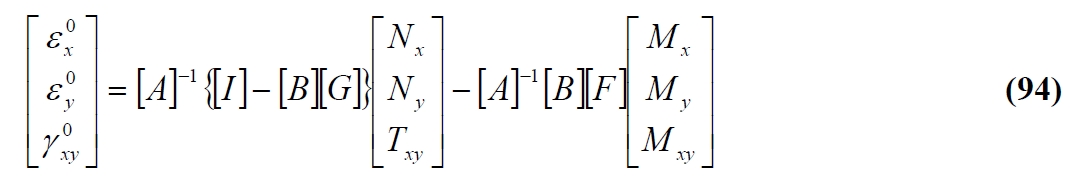
Where indicating with:

The (94) can be rewritten:
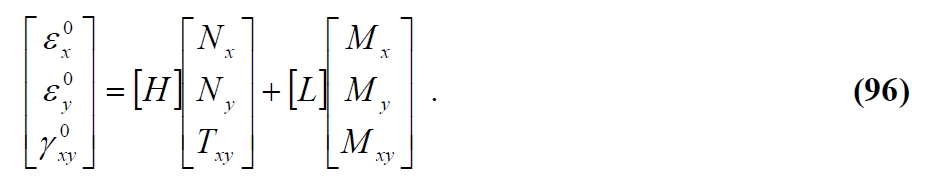
Finally bringing together (93) and (96) in a single equation we have:

With:
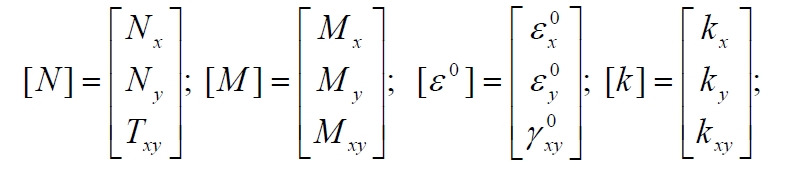
With these last equations it is possible to calculate the 6 strain components by simple manipulation (by inversion and multiplication) of matrices of 3×3 order. Once the strain components in the middle plane are calculated, it is possible to calculate the deformations and tensions (in the Cartesian reference x-y) at each point through the following eq.:
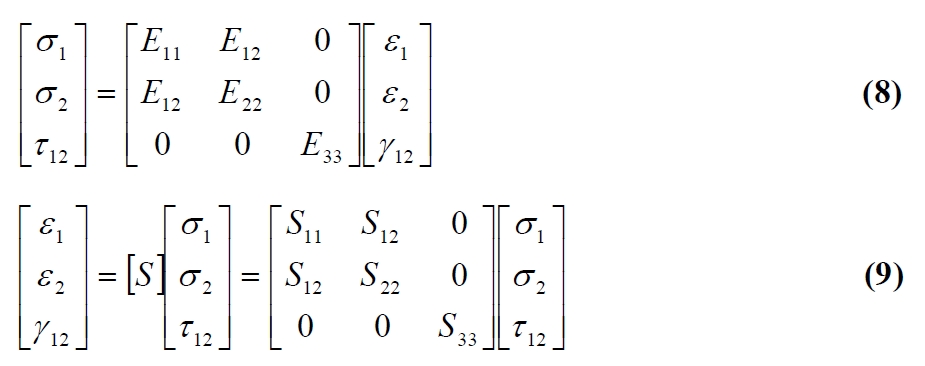
So for each lamina, the deformations and tensions in the main local reference can be finally calculated (as is necessary in the strength verification) by means of subsequent rotation of the deformations and tensions performed using an appropriate rotation matrix. In particular, if you want to calculate the stresses in the local reference, then is convenient to evaluate, for each ply, only the deformation in the Cartesian reference through equation (8), and then turn these components into the main reference by means of the rotation matrix, and finally calculate the stresses in the main reference by the constitutive equations of orthotropic lamina (eq. (8)).