1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Matrix of Elasticity
1.4. Matrix of Elasticity
 
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants

 >> Composite Analysis Tool

As is well known, a change of temperature induces generally in a material a deformation ε_t proportional to the coefficient of expansion α and the temperature variation Δt: ε_t=α Δt. For an anisotropic material the deformation varies with the direction since the coefficient of expansion varies with direction. For an orthotropic materia with unidirectional reinforcement there are two linear thermal expansion coefficients, αL and αT respectively in the longitudinal and transverse directions. For the symmetry, a change of temperature does not produce distortions in the main reference of material, the main deformations due to a temperature are:

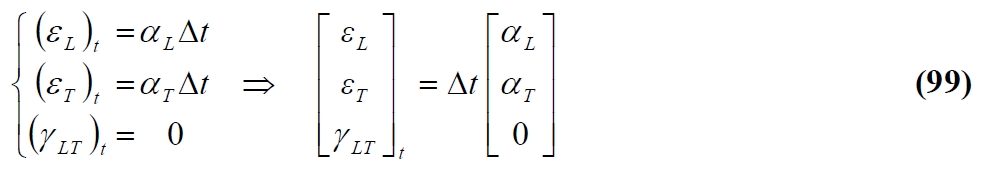
Like to the mechanical deformations, thermal deformations in a generic cartesian reference are obtained from the main by simple rotation. So:

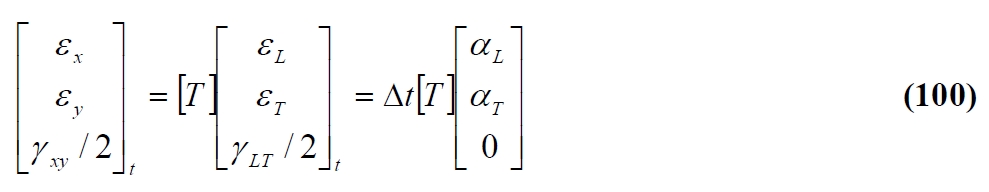
Dividing by Dt and defining α_xy = γ_xy / Δt from (100) we obtain:

Therefore:

for the (101), and taking into account the expression of the rotation matrix:

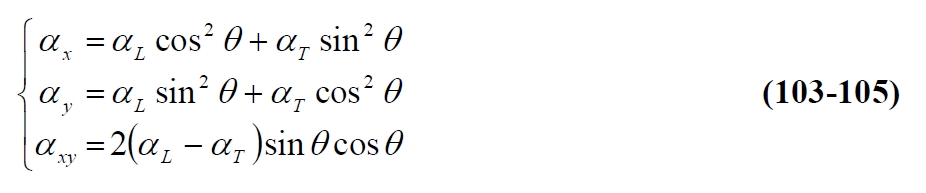
From (105), contrary to what occurs in an isotropic material, in an anisotropic a temperature variation produces, in any cartesian reference different to the main (θ = 0°, θ = 90 °), dilations and angular deformations. By the linear thermal expansion coefficients αL and αT, the (102) allows to evaluate the deformations of free ply  with a temperature variation Dt. With these deformations (expansion) there are no macroscopic thermal tensions if the ply is free to deform. We have only internal tensions due to the different expansion of fiber. If the ply instead belongs to a laminate then it is not completely free to deform due to the presence of other plys with different orientation. In other words the presence of the other plys induces a mechanical deformation εm equal to the difference between the effective strain ε and the thermal deformation εt. Taking into account the equations of laminate classical theory:

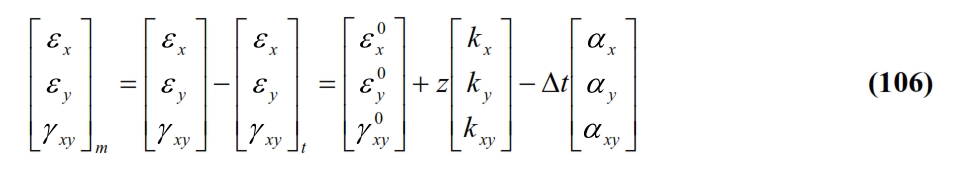
The mechanical deformations of the lamina are associated (through constituent equations) to the corresponding thermal stresses:

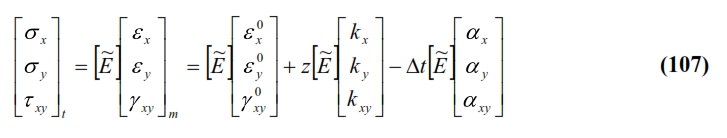
For the calculation of the thermal stresses, it is necessary to evaluate the deformation components of the the middle plane of the laminate. These can be evaluated taking into account that thermal stresses, in absence of external loads applied to the laminate, makes up an auto-balanced system with force resultant and momentum equal to zero. Therefore, the stress characteristics will be null. From the definition of the latter, and by using the matrices [A], [B] and [D], and the equation (107) we have:

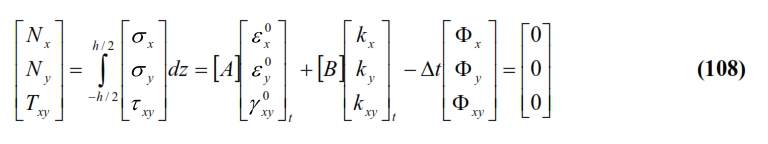
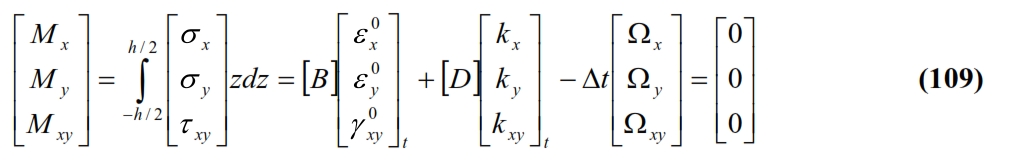
Where:

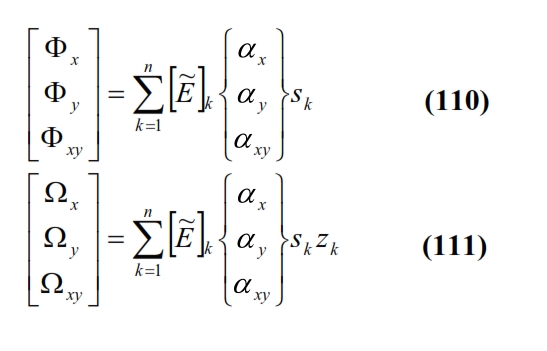
The equations (108) and (109) together with (110-111), allow to define the “apparent” thermal stress characteristics, also known as thermal forces and thermal moments, that allow to evaluate the thermal deformations in the planes with similar formulas to those already menthined for mechanical stresses. Thus we have:

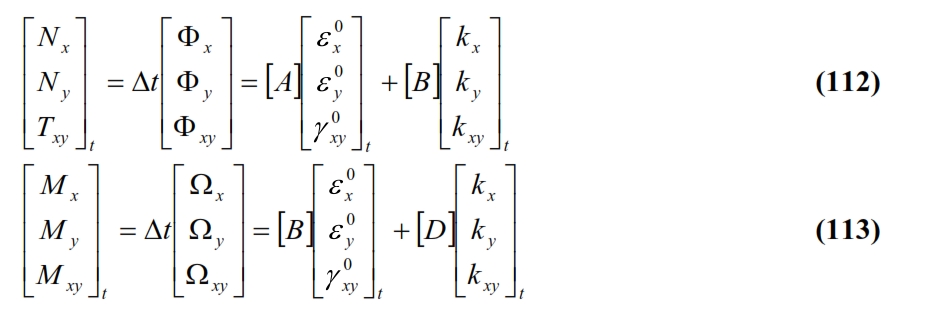
The (112-113) show how a temperature variation Δt induces in a generic laminate, normal stress and bending stresses, or in terms of deformations, both dilations and curvature and distortions. The curvatures of the middle plane are nil only if the laminate has matrix [B] = 0, that it means the laminate is symmetrical in this case. Therefore in a non-symmetrical laminate, the inevitable variations of the temperature you have during cooling of the treatment temperature (often higher than 100 ° C) at room temperature produce annoying distortions. Symmetry eliminates distortions but not thermal residual stresses, which can be calculated using the constituent equation (8):

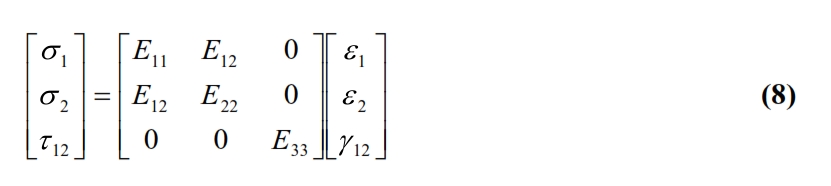
The residual thermal tensions are added to the operating tensions affecting the resistance and the laminate stability. For a proper and accurate design it is therefore necessary to take into account of residual stresses in the laminate. At the thermal stresses above calculated, due essentially to the fact that the dilations heat of each lamina are partially prevented by the other laminae, it is necessary to add the “internal” residual thermal stresses, that occours also in a single free ply due to of  different linear thermal expansion coefficient between fiber and matrix. Since the thermal expansion coefficient of matrix is always higer than that of the fibers, the cooling of the laminate produces a tension in the matrix parallel to the fibers, and compressions orthogonal to the fibers.  For the fiber and matrix can be defined the following initial averaged tensions:

In an orthogonal plane to the fibers, the matrix tends to contract more than the fibers, exerciting compression on the fibers (the matrix incorporates the fibers). This compression stress at the interface produces beneficial effects on the strength of the laminate as it ensures a good transmission of stress between fibers and matrix even in the absence of a good bonding due to the presence of beneficial friction forces on the fiber-matrix interface.