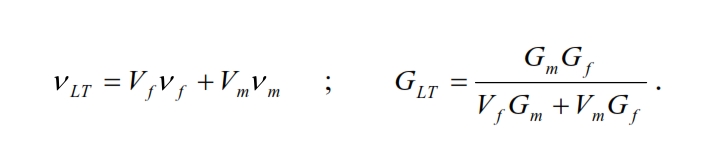1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Elasticity Matrix 
1.4. Matrix of Elasticity
 
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants

 >> Composite Analysis Tool

Consider an element of the laminate as depicted in Figure below, suppose that composite is subjected to deformation εL in the direction of the fibers. The fiber will be stressed by a tension:

σ_f= E_f  ·ε_L

while the matrix is subjected to a stress tension equal to:

σ_m= E_m  ·ε_m

where E_f  and E_m are respectively the Young module of the fibers and matrix.

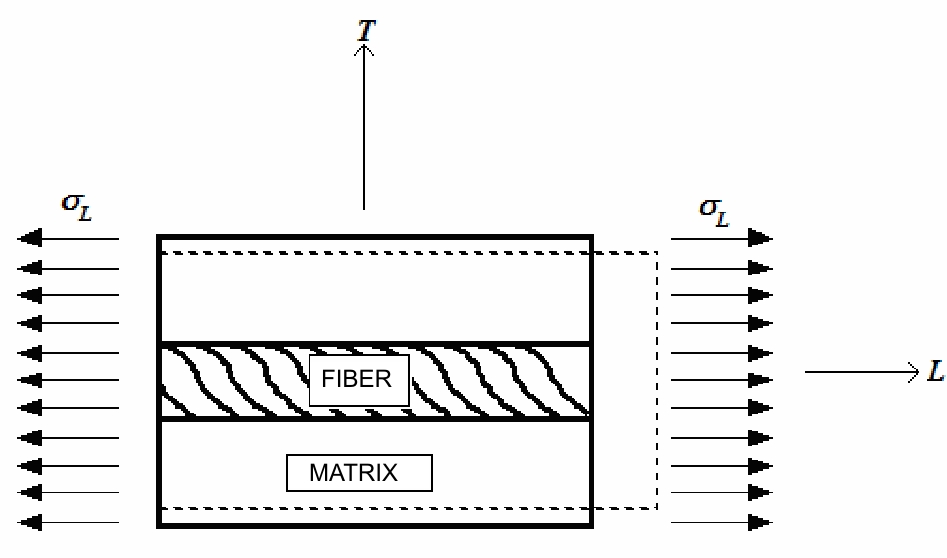
Unit volume of laminate loaded along the direction of the fibers (L)

The area section A of unit volume of laminate (ortogonal to L direction, see figure above) is subjected to stress tension σ_L in order to this equivalence is valid:

P=σ_f  ·A_f = σ_f  ·A_f + σm ·A_m

Since σ_f= E_f  ·ε_L, then:

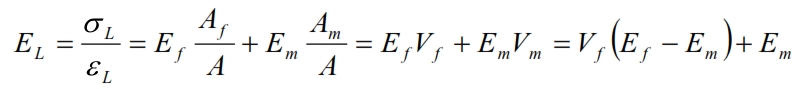
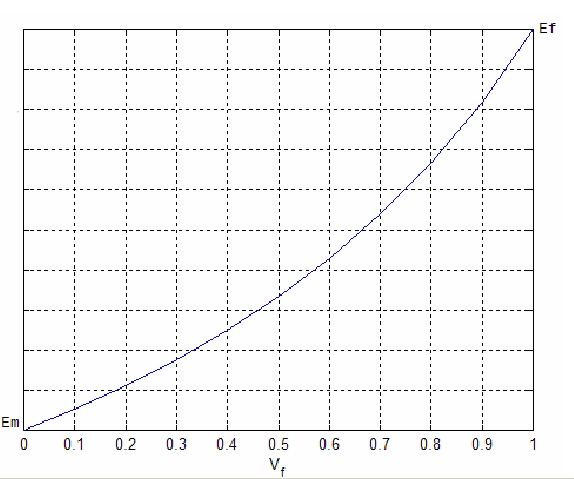
This formula of Young module rapresents a linear variation of E_L, from  E_m to E_f, when V_f varies from 0 to 1 (see figure below).

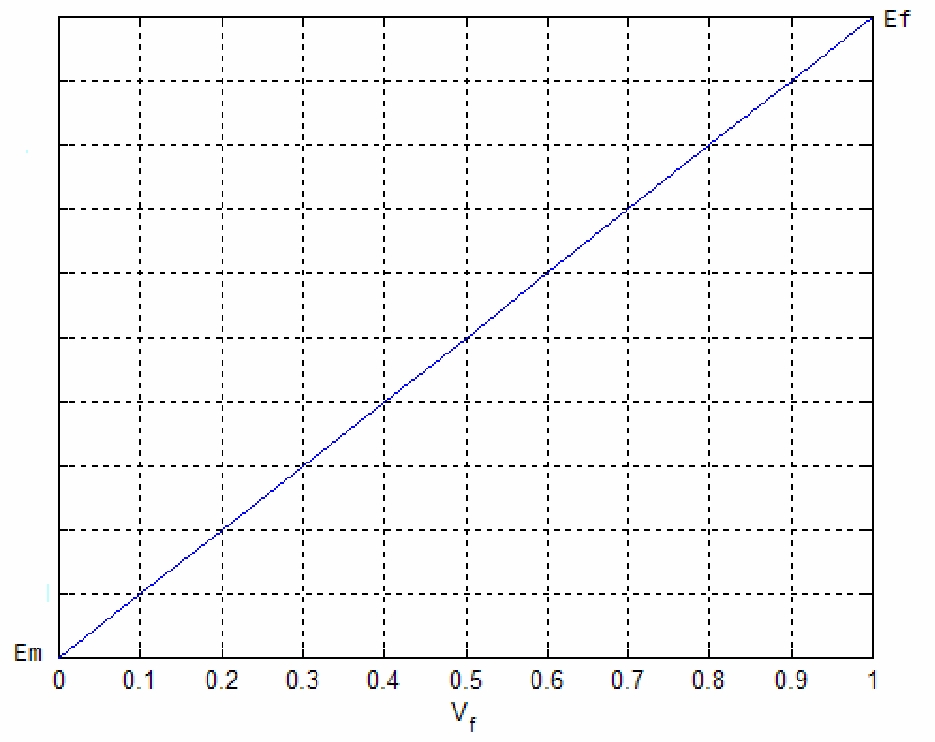
Trend of young moduLe EL as a function of percentage of fibers in the unit volume

Young’s module in the T direction can be considered considering the same fundamental volume element of the of the plate, loaded with a stress σT (Figure below).

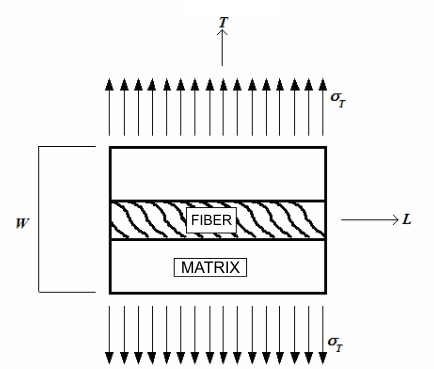
The deformation in the T direction for the matrix is:

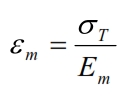
The deformation for the fiber is:

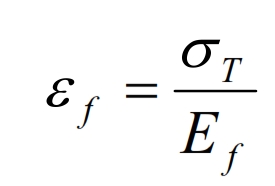
The trasversal area where ε_L is applied is approximatively V_fW, while for ε_m is VmW. The total deformation is:  ε_T ·W=V_f ·W·ε_L + Vm·W· ε_L è  ε_T =V_f ·ε_L + Vm· ε_L

Then using the previous formulas of ε_L and ε_T:

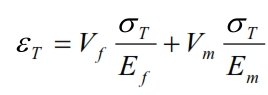
Thus:

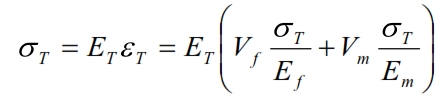
By means can be calculated the Young module in the T direction:

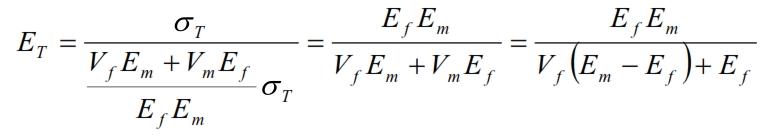
With similar considerations, we can derive the values of the Poisson coefficients and the tangential module: