A structure is labile if is possible to have a rigid cinematism, it is isostatic if is possible to calculate the reaction forces by the static equilibrium equations only, and it is statically indeterminate if it has an overabundance of constraints, and the equations of static are not sufficient for the determination of the reactions.
To classify a structure if it is labily or hyperstatic in the most of cases is enough count the rigids parts t divided by the constraints, counting the s degree of freedom suppressed by the constraints (internal and external), and evaluate the difference:
3 t – s < 0 -> Hypestatic
3 t – s = 0 <- Isostatic
3 t – s > 0 -> labile
The second equation can implies lability and/or isostatic condition, in this case is necessary a deeper study of the structure to understand which category belongs the structure.
Sometimes the constraints presence is unuseful, below are shown 2 examples.
Exemple 1
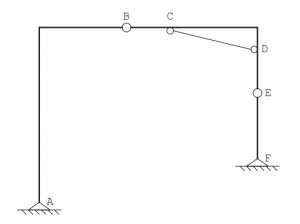
The structure shown below consists of three rigid parts connected each together with two hinges B and E, and to the ground with two supports at A and F. Without the pendulum CD, the structure is clearly labile, infact as has 3t = 9 degrees of freedoms, and can only be written s = 8 constraint equations. Introducing the pendulum CD, it also introduces a constraint equation, thus 3t-s = 0, and the structure is potentially isostatic. However, if the pendulum connects two points of the same rigid point, it is ineffective. As consequence the structure is labile and hyperstatic in the same time.
Exemple 2
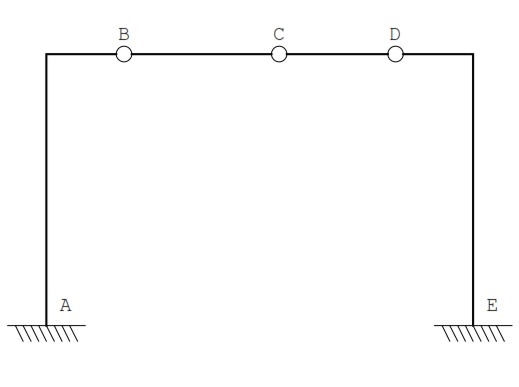
The structure below is blocked at ona foot, and it has three hinges to divide the structure into four sections. By making a first computation of the constraints, it leads to write 3t = 12 and s = 12, then the isostatic condition is satisfied, 3t – s = 0. However, the presence of three hinges aligned along the transverse implies the possibility of a lowering to the central hinge, and therefore the structure is isostatic and indeterminate at the same time
Moltiple constraints
a) Internal hinge with n rods: the supressed DOF (degree of freedom) are equal to 2(n-1)
b) Hybrid hinge type 1: 2n-1 supressed DOF
c) constraint plus carriage: 3n-2 supressed DOF
Cases with simpler formula:
Beam without orizontal forces
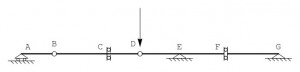
Below is shown a beam subject to transverse forces and / or couples concentrated agents in the plane of the beam, the forces acting along the axis of the beam are zero. In this case, the equations of equilibrium to the horizontal translation is automatically satisfied, and each translation can be written two equations of equilibrium. Correspondingly, the constraints have to be rethought, eliminating from the calculation of the degrees of freedom ‘suppressed those related to horizontal displacements; it follows that disappears the difference between support and trolley sliding plane horizontal, that a hinge internal is defined by two vertical forces equal and opposite, which reacts with an internal double pendolo two couples of forces, the joint eliminates two degrees of freedom, and so on. In this case instead of 3t-s can be used 2t-s, so the structure is lable with 1 DOF.
Truss
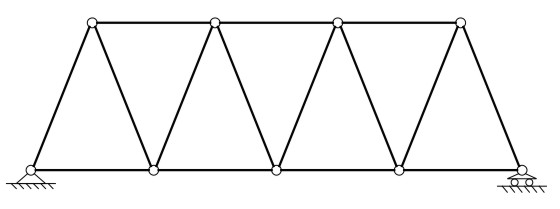
In this case is possible to simplify the calculation considering the truss as several concentrated points c, and the hinges are connected by n rods that are like pendols. The structure without the constraints have 2c DOF, to whom have to be subtracted a DOF of the internal constraints, and the v DOF of the external constraints. Thus we have this formula:
2c-a-v = l – h
In this case thus we have c = 9, a=15 ,v= 3, conseguently 2c-a-v = 0