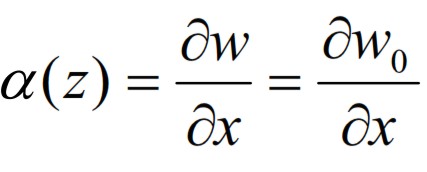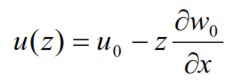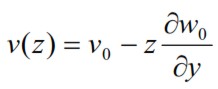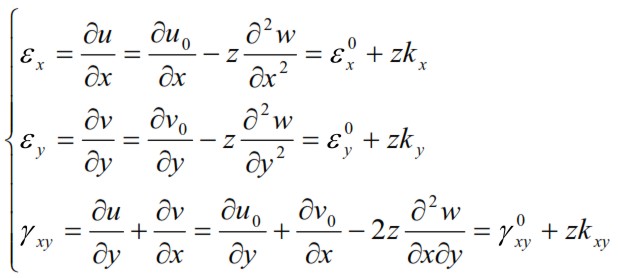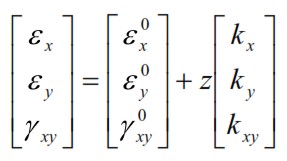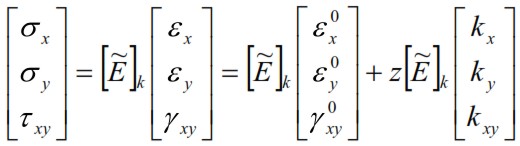1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Matrix of Elasticity
1.4. Matrix of Elasticity
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants
>> Composite Analysis Tool
The performance in terms of deformations and stresses in a composite laminate can be easily obtained by some simplifying assumptions:
1) The laminas forming the laminate are perfectly pasted so that no mutual sliding can occur under the action of applied loads (continuity of displacements and deformations at the interface between two adjacent foils);
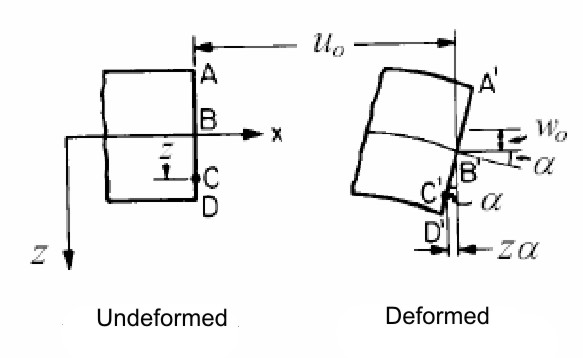
2) The generic straight line segment perpendicular to the middle plane of the laminate (see Figure 1) remains rectilinear and orthogonal to the mean plane also to deformation occurred: γxz=γyz=0;
3) The deformation ɛz is small and negligible with respect to the others deformations ɛx and ɛy.
4) the thickness of the laminate is small with respect to the other dimensions.
The hypothesis is generally well satisfied by commercial composite laminates, since the thickness of the adhesive used is very small compared to the size of the plates. Moreover, in a laminate with a thickness small compared to the other dimensions, the hypotheses 2 and 3 are satisfied mainly in areas distant from the applied loads and from the edges.
Under these assumptions, considering a generic straight line segment perpendicular to the median plane, and denoting with u0, v0 and w0 the components along the x, y, and z of the displacement from the point on the median plane, the displacement u along x for the generic point located on the line with a distance of z from the median plane is equal to:
u(z)=uo-αz
with α the rotation of the segment. Taking in to account these hypotesis the this rotation is linked to the displacement z:
Replacing the (60) in the (59):
rotation is linked to the displacement along z from the relation:
Using the congruence equations for the deformations in the xy plane we obtain the following expressions:
The kx, ky and kxy, the curvatures of the mid-plane of the laminate in the planes x-z,y-z and x-y. The (63-65) can be written in matrix form as:
Equation (66) shows that significant strain components all vary linearly in the thickness z of the laminate. The strains vary linearly along z, but it does not occur usually for the tensions. In each lamina of the laminate, in fact they are related to the deformation of the stress-strain relationships (see Analysis of the Orthotropic Lamina). For the k-th lamina:
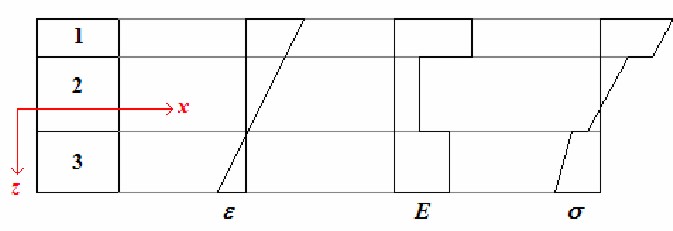
Taking into account that the matrix ![]() varies from one lamina to the other depending only by the peculiar characteristics of the lamina, by the relative orientation, by the (67) we can observe that the tensions in despite of the deformations are linear in Generic section of the laminate, but typically exhibit jumps passing from one plate to another.
varies from one lamina to the other depending only by the peculiar characteristics of the lamina, by the relative orientation, by the (67) we can observe that the tensions in despite of the deformations are linear in Generic section of the laminate, but typically exhibit jumps passing from one plate to another.
The trend is instead linear within each lamina. The following figure shows the qualitative trend of a possible distribution of the stresses in a laminate builded up of three overlapping sheets.