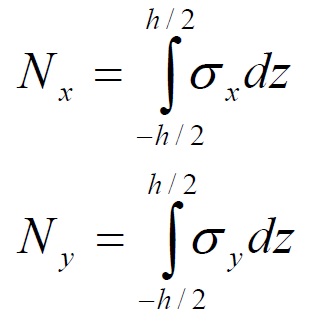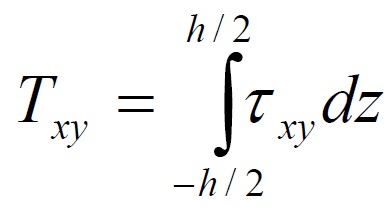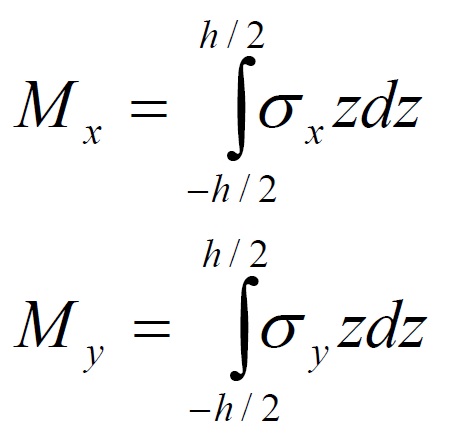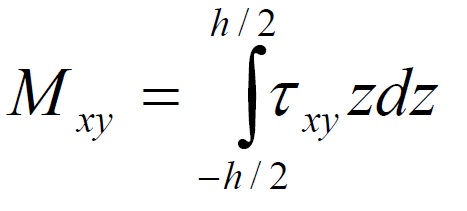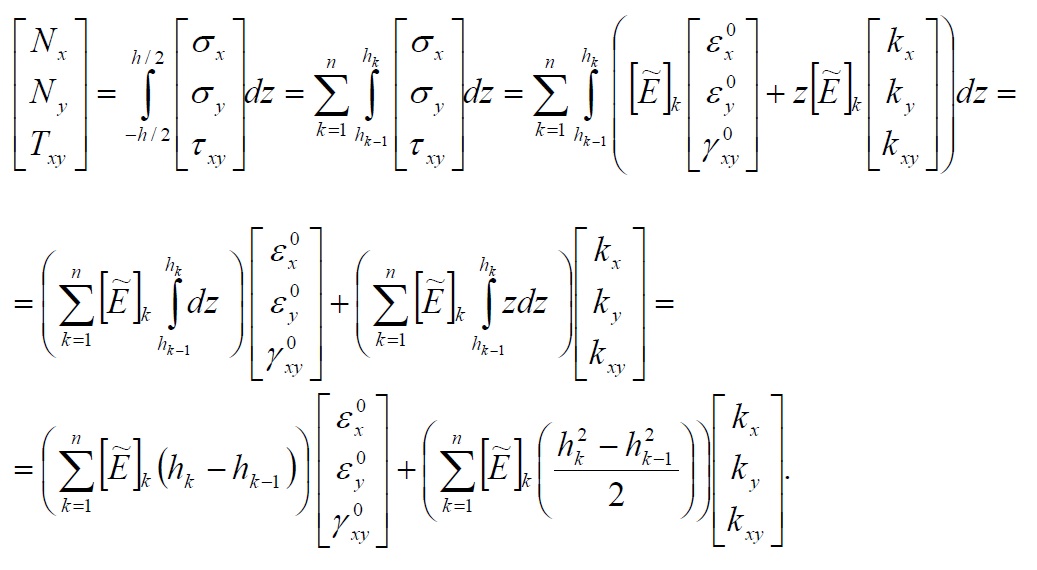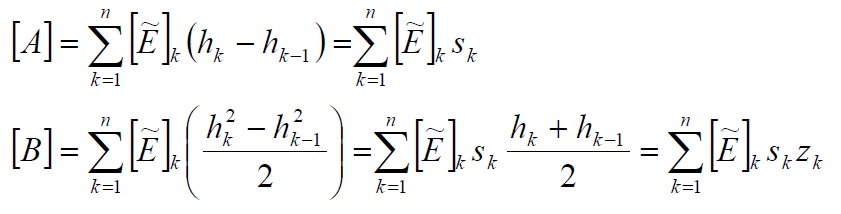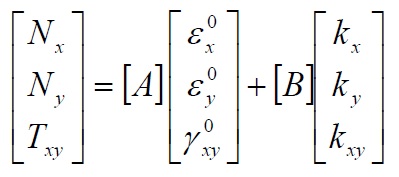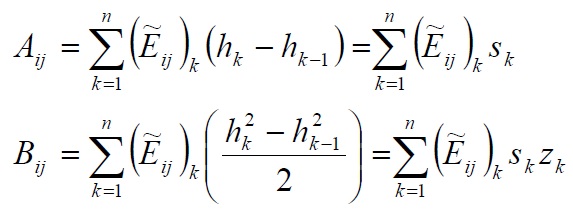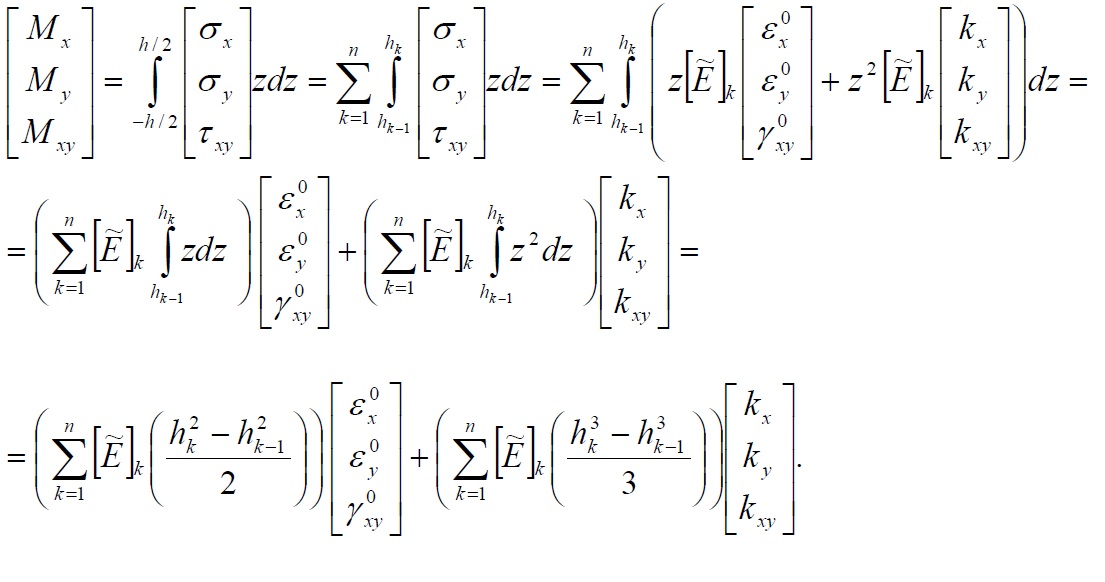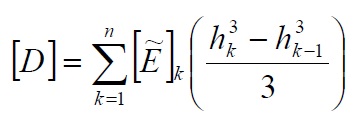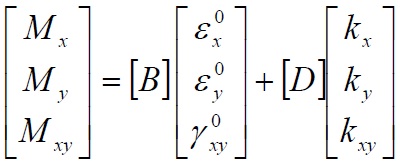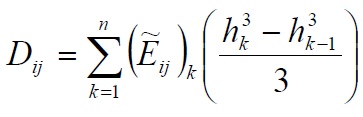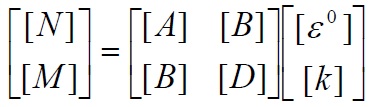1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Matrix of Elasticity
1.4. Matrix of elasticity
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants
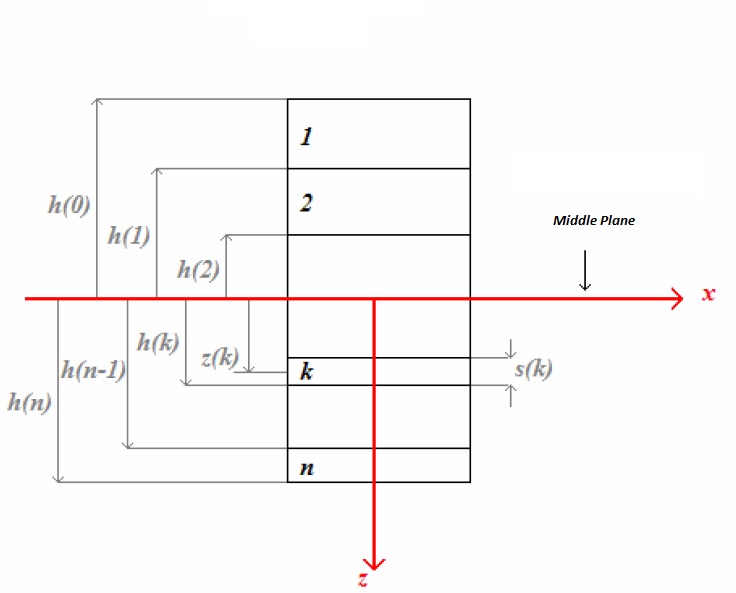
The equations (66), link the tensions in each lamina with corresponding deformations and curves in the middle plane of the laminate. From these equations is possible (in the matrix form) to get the relationship between the stress (for unit length, normal stress, torque and bending) and the deformation component in the middle plane. The general case of laminat with n plaies is considered, see the figure below.
For the equilibrium, the cartesian components of the normal stress (for length unit) are:
The Shear in the plane is equal to:
For the bending moment we have:
and for the Torque moment:
Replacing in the (68-73) the general relation (67) and taking in to account of the integral properties for the normal and shear stress we have:
Posing [A] and [B] equal to:
We have:
Since the elements of the matrix [A] and [B] are equal to:
Instead for the torque and bending moment we have:
Posing [D] equal to:
Thus we have:
Sine the elements of the [D] matrix are equal to:
Finally the (77) and (82) can be joint in an unique matricial expression:
With
The (84) rappresents the constitutive equation of the laminate. The matriy [A], [B] and [D] are named rispectively stiffener extension matrix, stiffener coupling matrix and stiffener flexural matrix.
The (77) shown that likely to a single lamina with a simple unidirectional normal stress that causes in general mainly a normal deformation but sliding deformation as well, and vice versa a shear stress causes mainly a sliding shear but a normal stress as well, in the composite laminate (with n laminates) a normal stress or a shear stress cause in general a plane deformation and flexural curvature and/or torque curvature in the middle plane.
This coupling effects are connected to the meccanichal caratteristics and lay-up sequence of the laminas, and not due for the anisotropy of the plies.
Indeed the [B] is not zero with isotrope laminates. The matrixs [A], [B] and [D] depend of the cartesian reference used. Consequently, likewise the coupling between normal deformations amd slidings depend of the direction, for a composite laminate the coupling between normal deformations amd curvatures depend of the load direction (in the composite could be some reference whereby [B] is identically zero.
SYMMETRIC LAMINATE ([B]=0)
In the symmetric laminate the coupling between bending and normal stress is eliminated. In these laminates the application of a normal force produces no bending of the average plane, and the application of a bending moment produces no deformation (extension / contraction) of the middle plane. This feature is very important, it avoids that the application of stresses in the plane of the laminate produces deformation out of the plane. Moreover, the absence of coupling, allows to prevent unpleasant eventual distortions due to cooling of the laminate after the cure. Taking into account the constitutive equations explained in above, such behavior of the laminate corresponds to the condition with matrix coupling [B] identically zero. Taking into account that the generic term of the matrix [B] is given by the summation (extended to the plies) of homologous terms of the matrix [Ẽ]k multiplied by the thickness of the plies and for the average distance from the mean plane (sk, z k), such terms can be equal to zero if at every ply placed above (or below) of the average plane corresponds an equal ply with identical orientation placed symmetrically with respect to the middle plane. In this case the laminate is defined as “symmetric”.
The symmetrical laminate is indicated with a code within square brackets, and only one half is shown due to its symmetry. The sequence starts from the mid laminate:
0°\0°\+45°\-45°\-45°\+45°\0°\0°
It is synthetically indicated with the code:
[02/±45]s.
In the case where the laminate is obtained by repeating m times a sequence of n plies, then its indication can be simplified in parentheses indicating the sequence and putting m as subscript. For example a laminate consisting of a sequence of plies 5:
0°\0°\+45°\-45°\90°
repeated 20 times (symmetric laminate) can be synthetically expressed as:
[(02/±45/90)10]s
SYMMETRICAL LAMINATES (ORTHOTROPIC LAMINATE, A13=A23=0)
This type of laminates present decoupling between normal and shearing stress or between normal and shear deformations. Considering the constitutive equation (already menthioned in above):
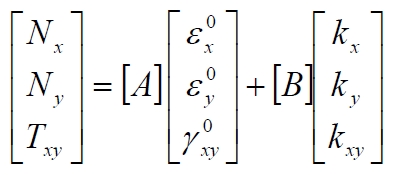
this condition is fulfilled if the terms A13 and A23 of the matrix [A] are equal zero. Taking into account that such terms are obtained as summation of homologues terms of the matrix [Ẽ]k multiplied for the thickness of each respective ply (constant for the same ply):
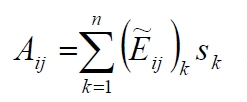
and since the terms [Ẽ]13 and [Ẽ]23 are odd functions of angle θ, so the terms A13 and A23 of the matrix [A] can be equal to zero, if the laminate is made up in the way that for each lamina with θ orientation corresponds an opposite laminate with orientation – θ., regardless of the sequence of a packaging:
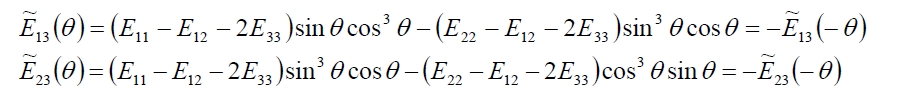
Obviously is possible to have a laminate with decoupling between normal stress and sliding, and symmetrical (decoupling between normal stresses or shear and curvatures). It is enough to positioning the plies in the manner to have the upper (bottom) half of laminate made up by plirs that satisfy A13 = A23 = 0, ie at a ply with θ orientation has to be correspond a ply with -θ orientation, and the upper part of the lamina has to be symmetrical to the lower part with respect the laminate’s middle. The decoupling between normal deformations and slidings (A13 = A23 = 0) depends on the direction of application of the load, so by reference system. As well as for the unidirectional lamina, for which the decoupling occurs only if the load acts along the main axes, for a Laminate happen only if the load is acting along the x-y axes so that it is A13 = A23 = 0. In other words the x-y axes for which is A13 = A23 = 0 in practice constitute the main axes of the laminate.
Considering the analytical expression of terms [Ẽ]13 and [Ẽ]23, and considering a new cartesian reference x’-y ‘rotated by an angle α (not equal to 0° or 90 °) respect the main reference x-y, we have:
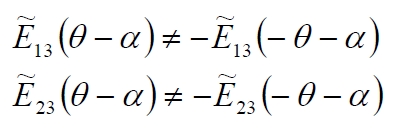
As example the symmetrical laminate mentioned in the preceding paragraph consists of all laminae 8 equal oriented according to the scheme [02 / ± 45] s is a laminate for which also true A13 = A23 = 0. The sequence of packaging has no importance, and therefore the orientation of each ply can be varied to fulfill additional requirements of the process or production. Symmetrical laminates with A13 = A23 = 0 are commonly known as orthotropic laminated, because admit three plane (x-y-z) of symmetry reciprocally orthogonal.
LAMINATES with D13≈D23≈0
Another considerable laminates class is the one that realizes the decoupling between stresses bending and torsional bending, and between the torque and bending curvatures. For these laminates a bending moment produces only a curvature of the laminate in-plane being null in the orthogonal plane. Considering the equaltion already menthioned in:
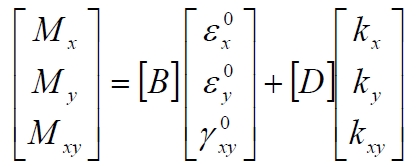
this condition is fulfilled if: D13 = D23 = 0. To have these terms equal to zero you has to be putting above and below the middle plane, laminates with opposite orientation. But this situation is not advantageous since the decoupling between normal stress and flexion is commonly requested (symmetric laminates). Nevertheless with successive sheets placed in opposite orientation, it is possible to get an array with elements D13 and D23 very small (being opposite counterparts terms of the stiffness matrix and the coefficients related to the cubes of the distances are equal), so that bending and torsion are almost decoupled. As for the previous case, and for the same reasons, the decoupling condition is closely linked to the orientation. We have that a symmetrical laminate obtained by packing pairs of successive sheets in the opposite orientation is a laminate that achieves the decoupling between normal and bending stress ([B] = 0), the decoupling between normal stress and angular sliding (A13 = A23 = 0), and also the decoupling between bending moment and bending out of the Stress plan (torsion). As an example, the laminate referred to in the previous paragraph [02 / ± 45] s realized in practice all three conditions, as is also the laminate [02 / ± 45/902] s.
LAMINATES Quasi -ISOTROPIC
Quasi-isotropic means “almost isotropic”, where a quasi-isotropic laminate is isotropic in stiffness in the plane of the material, but not isotropic in strength nor is it isotropic through the thickness or in bending. They have isotropic behavior only with respect to the traction-compression and not with respect to bending and torsion being in general the other matrices [B] and [D] not isotropic. Quasi-isotropic laminates can be made with both unidirectional and woven fabric plies. Unidirectional quasi-isotropic laminates are made from a c laminate of 0/+60/-60 and 0/90/+45/-45 plies that can be laminated in any order as long as the laminate is symmetric (mirror image about the laminate midplane) and balanced (equal numbers of +angle and -angle plies).The result is a laminate that has the same inplane stiffness in all directions. However the laminate will not have the same bending stiffness in all directions, nor will necessarily have the same strength in all directions (depending of the failure criteria used). Quasi-isotropic laminates are good for applications where the exact orientation of the load is not known. However, the true benefit of composites is to tailor the strength and stiffness to only directions where it is required, such that a quasi-isotropic laminate may provide stiffness is directions where it is not required, which defeats the purpose of using composites to start with. A fourth class of particular laminates consists of the so-called quasi-isotropic laminates. A laminate is said quasi isotropic if in practice its extensional stiffness is considered independent of the particular orientation, in other words the matrix [A] is isotropic.
To obtain that extensional stiffness is independent of the orientation, considering that the terms of the matrix [A] are given by the sum of each product of the counterpart terms of the matrices [E]k multiplied with thickness of each ply (equal thickness for each ply), it is necessary that the sum of both counterpart terms have to be invariant with respect to a reference rotation. In other words must be verified following conditions:
- 1) – the total number n of plies are greater than or equal to 3;
- 2) – the plies have the same constitution and thickness;
- 3) – the angle Δθ between two plates is constant, ie Δθ = 360 ° / n (plies angularly equally spaced);
With proper orientation of the plies is possible to obtain an Quasi-isotropic laminate with respects several decoupling conditions. For example a symmetrical laminate consisting of laminae 12 arranged according to the scheme [(± 30 / ± 90 / ± 30) 6]s. Indeed half of the laminate is built up by 6 laminae equally angularly spaced of 60 ° and also the adjacent couple laminae have opposite orientation, so that also satisfy decoupling conditions: A13 = A23=0, D13=D23 =0. The quasi-isotropic laminates are not widely used because the optimal exploitation of the composites is based precisely on the anisotropy that allows to suitably orient the plies in order to obtain the maximum strength in the desidered direction. The theory of quasi-isotropic laminate is still useful for the prediction of the characteristic properties (stiffness and strength) of composite short fibers with random orientation. The properties of such composites may for example be well approximated by considering the simple laminate [0°/± 60].