Orbit Meccanics:
- 1) Conic Sections
- 2) Orbital Elements
- 3) Types of Orbits
- 4) Newton’s Laws of Motion and Universal Gravitation
- 5) Uniform Circular Motion
- 6) Motions of Planets and Satellites
- 7) Launch of a Space Vehicle
- 8) Position in an Elliptical Orbit
- 9) Orbit Perturbations
- 10) Orbit Maneuvers
The launch of a satellite or space vehicle consists of a period of powered flight during which the vehicle is lifted above the Earth’s atmosphere and accelerated to orbital velocity by a rocket, or launch v
ehicle. Powered flight concludes at burnout of the rocket’s last stage at which time the vehicle begins its free flight. During free flight the space vehicle is assumed to be subjected only to the gravitational pull of the Earth. If the vehicle moves far from the Earth, its trajectory may be affected by the gravitational influence of the sun, moon, or another planet.
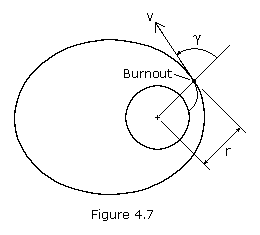
A space vehicle’s orbit may be determined from the position and the velocity of the vehicle at the beginning of its free flight. A vehicle’s position and velocity can be described by the variables r, v, and ![]() , where r is the vehicle’s distance from the center of the Earth, v is its velocity, and
, where r is the vehicle’s distance from the center of the Earth, v is its velocity, and ![]() is the angle between the position and the velocity vectors, called the zenith angle (see Figure 4.7). If we let r1, v1, and
is the angle between the position and the velocity vectors, called the zenith angle (see Figure 4.7). If we let r1, v1, and ![]() 1 be the initial (launch) values of r, v, and
1 be the initial (launch) values of r, v, and ![]() , then we may consider these as given quantities. If we let point P2represent the perigee, then equation (4.13) becomes:
, then we may consider these as given quantities. If we let point P2represent the perigee, then equation (4.13) becomes:
![]()
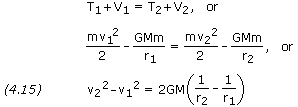
![]()
Substituting equation (4.23) into (4.15), we can obtain an equation for the perigee radius Rp.
![]()
Multiplying through by -Rp2/(r12v12) and rearranging, we get
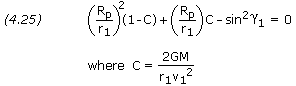
Note that this is a simple quadratic equation in the ratio (Rp/r1) and that 2GM /(r1 × v12) is a nondimensional parameter of the orbit.
Solving for (Rp/r1) gives
![]()
Like any quadratic, the above equation yields two answers. The smaller of the two answers corresponds to Rp, the periapsis radius. The other root corresponds to the apoapsis radius, Ra.
Please note that in practice spacecraft launches are usually terminated at either perigee or apogee, i.e. ![]() = 90. This condition results in the minimum use of propellant.
= 90. This condition results in the minimum use of propellant.
PROBLEM 1 A satellite is launched into Earth orbit where its launch vehicle burns out at an altitude of 250 km. At burnout the satellite's velocity is 7,900 m/s with the zenith angle equal to 89 degrees. Calculate the satellite's altitude at perigee and apogee. SOLUTION, Given: r1 = (6,378.14 + 250) × 1,000 = 6,628,140 m v1 = 7,900 m/s= 89o Equation (4.26), (Rp / r1)1,2 = ( -C ± SQRT[ C2 - 4 × (1 - C) × -sin2
]) / (2 × (1 - C)) where C = 2 × GM / (r1 × v12) C = 2 × 3.986005×1014 / (6,628,140 × 7,9002) C = 1.927179 (Rp / r1)1,2 = ( -1.927179 ± SQRT[ 1.9271792 - 4 × -0.927179 × - sin2(89) ]) / (2 × -0.927179) (Rp / r1)1,2 = 0.996019 and 1.082521 Perigee Radius, Rp = Rp1 = r1 × (Rp / r1)1 Rp = 6,628,140 × 0.996019 Rp = 6,601,750 m Altitude @ perigee = 6,601,750 / 1,000 - 6,378.14 = 223.6 km Apogee Radius, Ra = Rp2 = r1 × (Rp / r1)2 Ra = 6,628,140 × 1.082521 Ra = 7,175,100 m Altitude @ agogee = 7,175,100 / 1,000 - 6,378.14 = 797.0 km
Equation (4.26) gives the values of Rp and Ra from which the eccentricity of the orbit can be calculated, however, it may be simpler to calculate the eccentricity e directly from the equation
![]()
PROBLEM 2 Calculate the eccentricity of the orbit for the satellite in problem 1. SOLUTION, Given: r1 = 6,628,140 m v1 = 7,900 m/s= 89o Equation (4.27), e = SQRT[ (r1 × v12 / GM - 1)2 × sin2
+ cos2
] e = SQRT[ (6,628,140 × 7,9002 / 3.986005×1014 - 1)2 × sin2(89) + cos2(89) ] e = 0.0416170
To pin down a satellite’s orbit in space, we need to know the angle ![]() , the true anomaly, from the periapsis point to the launch point. This angle is given by
, the true anomaly, from the periapsis point to the launch point. This angle is given by
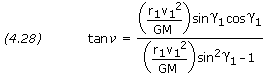
PROBLEM 3 Calculate the anglefrom perigee point to launch point for the satellite in problem 1. SOLUTION, Given: r1 = 6,628,140 m v1 = 7,900 m/s
= 89o Equation (4.28), tan
= (r1 × v12 / GM) × sin
× cos
/ [(r1 × v12 / GM) × sin2
- 1] tan
= (6,628,140 × 7,9002 / 3.986005×1014) × sin(89) × cos(89) / [(6,628,140 × 7,9002 / 3.986005×1014) × sin2(89) - 1] tan
= 0.48329
= arctan(0.48329)
= 25.794o
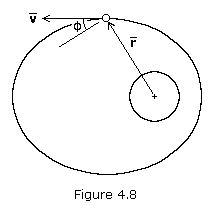 In most calculations, the complement of the zenith angle is used, denoted by
In most calculations, the complement of the zenith angle is used, denoted by ![]() . This angle is called the flight-path angle, and is positive when the velocity vector is directed away from the primary as shown in Figure 4.8. When flight-path angle is used, equations (4.26) through (4.28) are rewritten as follows:
. This angle is called the flight-path angle, and is positive when the velocity vector is directed away from the primary as shown in Figure 4.8. When flight-path angle is used, equations (4.26) through (4.28) are rewritten as follows:
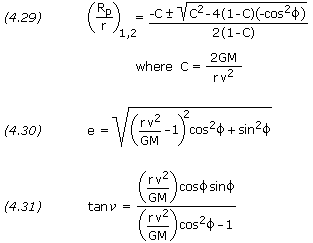
The semi-major axis is, of course, equal to (Rp+Ra)/2, though it may be easier to calculate it directly as follows:
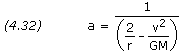
PROBLEM 4 Calculate the semi-major axis of the orbit for the satellite in problem 1. SOLUTION, Given: r1 = 6,628,140 m v1 = 7,900 m/s Equation (4.32), a = 1 / ( 2 / r1 - v12 / GM ) a = 1 / ( 2 / 6,628,140 - 7,9002 / 3.986005×1014) ) a = 6,888,430 m
If e is solved for directly using equation (4.27) or (4.30), and a is solved for using equation (4.32), Rp and Ra can be solved for simply using equations (4.21) and (4.22).
Orbit Tilt, Rotation and Orientation
Above we determined the size and shape of the orbit, but to determine the orientation of the orbit in space, we must know the latitude and longitude and the heading of the space vehicle at burnout.
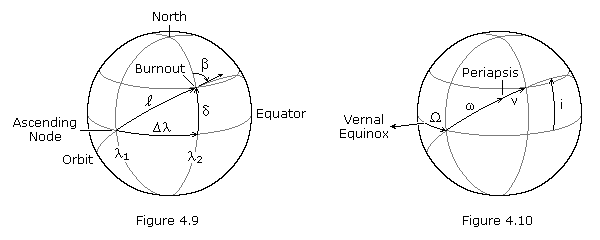
If ![]() ,
, ![]() , and
, and ![]() 2 are given, the other values can be calculated from the following relationships:
2 are given, the other values can be calculated from the following relationships:
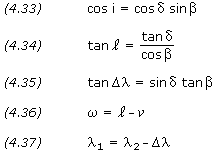
In equation (4.36), the value of ![]() is found using equation (4.28) or (4.31). If
is found using equation (4.28) or (4.31). If ![]() is positive, periapsis is west of the burnout point (as shown in Figure 4.10); if
is positive, periapsis is west of the burnout point (as shown in Figure 4.10); if ![]() is negative, periapsis is east of the burnout point.
is negative, periapsis is east of the burnout point.
The longitude of the ascending node, ![]() , is measured in celestial longitude, while
, is measured in celestial longitude, while ![]() 1 is geographical longitude. The celestial longitude of the ascending node is equal to the local apparent sidereal time, in degrees, at longitude
1 is geographical longitude. The celestial longitude of the ascending node is equal to the local apparent sidereal time, in degrees, at longitude ![]() 1 at the time of engine burnout. Sidereal time is defined as the hour angle of the vernal equinox at a specific locality and time; it has the same value as the right ascension of any celestial body that is crossing the local meridian at that same instant. At the moment when the vernal equinox crosses the local meridian, the local apparent sidereal time is 00:00. See this sidereal time calculator.
1 at the time of engine burnout. Sidereal time is defined as the hour angle of the vernal equinox at a specific locality and time; it has the same value as the right ascension of any celestial body that is crossing the local meridian at that same instant. At the moment when the vernal equinox crosses the local meridian, the local apparent sidereal time is 00:00. See this sidereal time calculator.
PROBLEM 5 For the satellite in problem 4.8, burnout occurs 2000-10-20, 15:00 UT. The geocentric coordinates at burnout are 32o N latitude, 60o W longitude, and the azimuth heading is 86o. Calculate the orbit's inclination, argument of perigee, and longitude of ascending node. SOLUTION, Given:= 86o
= 32o
2 = -60o From problem 4.10,
= 25.794o Equation (4.33), cos(i) = cos(
) × sin(
) cos(i) = cos(32) × sin(86) i = 32.223o Equations (4.34) and (4.36), tan(
) = tan(
) / cos(
) tan(
) = tan(32) / cos(86)
= 83.630o
=
-

= 83.630 - 25.794
= 57.836o Equations (4.35) and (4.37), tan(
) = sin(
) × tan(
) tan(
) = sin(32) × tan(86)
= 82.483o
1 =
2 -
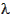
1 = -60 - 82.483
1 = -142.483o
= Sidereal time at -142.483 longitude, 2000-10-20, 15:00 UT
= 7h 27' 34" = 111.892o