Orbit Meccanics:

• 1)    Conic Sections
• 2)    Orbital Elements
• 3)    Types of Orbits
• 4)    Newton’s Laws of Motion and Universal Gravitation
• 5)    Uniform Circular Motion
• 6)    Motions of Planets and Satellites
• 7)    Launch of a Space Vehicle
• 8)    Position in an Elliptical Orbit
• 9)    Orbit Perturbations
• 10) Orbit Maneuvers

Johannes Kepler was able to solve the problem of relating position in an orbit to the elapsed time, t-t_o, or conversely, how long it takes to go from one point in an orbit to another. To solve this, Kepler introduced the quantity M, called the mean anomaly, which is the fraction of an orbit period that has elapsed since perigee.  The mean anomaly equals the true anomaly for a circular orbit. By definition,

where M_o is the mean anomaly at time t_o and n is the mean motion, or the average angular velocity, determined from the semi-major axis of the orbit as follows:

This solution will give the average position and velocity, but satellite orbits are elliptical with a radius constantly varying in orbit. Because the satellite’s velocity depends on this varying radius, it changes as well. To resolve this problem we can define an intermediate variable E, called the eccentric anomaly, for elliptical orbits, which is given by

where  is the true anomaly. Mean anomaly is a function of eccentric anomaly by the formula

For small eccentricities a good approximation of true anomaly can be obtained by the following formula (the error is of the order e³):

The preceding five equations can be used to (1) find the time it takes to go from one position in an orbit to another, or (2) find the position in an orbit after a specific period of time. When solving these equations it is important to work in radians rather than degrees, where 2 radians equals 360 degrees.

PROBLEM 4.13

A satellite is in an orbit with a semi-major axis of 7,500 km and an eccentricity
of 0.1.  Calculate the time it takes to move from a position 30 degrees past perigee
to 90 degrees past perigee.

SOLUTION,

   Given:  a = 7,500 × 1,000 = 7,500,000 m
           e = 0.1
           tO = 0
           O = 30 deg × /180 = 0.52360 radians 
            = 90 deg × /180 = 1.57080 radians

   Equation (4.40),

      cos E = (e + cos ) / (1 + e cos )

      Eo = arccos[(0.1 + cos(0.52360)) / (1 + 0.1 × cos(0.52360))]
      Eo = 0.47557 radians

      E = arccos[(0.1 + cos(1.57080)) / (1 + 0.1 × cos(1.57080))]
      E = 1.47063 radians

   Equation (4.41),

      M = E - e × sin E

      Mo = 0.47557 - 0.1 × sin(0.47557)
      Mo = 0.42978 radians

      M = 1.47063 - 0.1 × sin(1.47063)
      M = 1.37113 radians

   Equation (4.39),

      n = SQRT[ GM / a3 ]
      n = SQRT[ 3.986005×1014 / 7,500,0003 ]
      n = 0.00097202 rad/s

   Equation (4.38),

      M - Mo = n × (t - tO)

      t = tO + (M - Mo) / n
      t = 0 + (1.37113 - 0.42978) / 0.00097202
      t = 968.4 s

PROBLEM 4.14

The satellite in problem 4.13 has a true anomaly of 90 degrees.  What will be the
satellite's position, i.e. it's true anomaly, 20 minutes later?

SOLUTION,

   Given:  a = 7,500,000 m
           e = 0.1
           tO = 0
           t = 20 × 60 = 1,200 s
           O = 90 × /180 = 1.57080 rad

   From problem 4.13,

      Mo = 1.37113 rad
      n = 0.00097202 rad/s

   Equation (4.38),

      M - Mo = n × (t - tO)

      M = Mo + n × (t - tO)
      M = 1.37113 + 0.00097202 × (1,200 - 0)
      M = 2.53755

 METHOD #1, Low Accuracy:

   Equation (4.42),

       ~ M + 2 × e × sin M + 1.25 × e2 × sin 2M
       ~ 2.53755 + 2 × 0.1 × sin(2.53755) + 1.25 × 0.12 × sin(2 × 2.53755)      
       ~ 2.63946 = 151.2 degrees

 METHOD #2, High Accuracy:

   Equation (4.41),

      M = E - e × sin E
      2.53755 = E - 0.1 × sin E

      By iteration, E = 2.58996 radians

   Equation (4.40),

      cos E = (e + cos ) / (1 + e cos )

      Rearranging variables gives,

      cos  = (cos E - e) / (1 - e cos E)

       = arccos[(cos(2.58996) - 0.1) / (1 - 0.1 × cos(2.58996)]
       = 2.64034 = 151.3 degrees

At any time in its orbit, the magnitude of a spacecraft’s position vector, i.e. its distance from the primary body, and its flight-path angle can be calculated from the following equations:

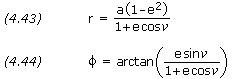
And the spacecraft’s velocity is given by,

PROBLEM 4.15

For the satellite in problems 4.13 and 4.14, calculate the length of its position
vector, its flight-path angle, and its velocity when the satellite's true anomaly
is 225 degrees.

SOLUTION,

   Given:  a = 7,500,000 m
           e = 0.1
            = 225 degrees

   Equations (4.43) and (4.44),

      r = a × (1 - e2) / (1 + e × cos ) 
      r = 7,500,000 × (1 - 0.12) / (1 + 0.1 × cos(225))
      r = 7,989,977 m

       = arctan[ e × sin  / (1 + e × cos )]
       = arctan[ 0.1 × sin(225) / (1 + 0.1 × cos(225))]
       = -4.351 degrees 

   Equation (4.45),

      v = SQRT[ GM × (2 / r - 1 / a)]
      v = SQRT[ 3.986005×1014 × (2 / 7,989,977 - 1 / 7,500,000)]
      v = 6,828 m/s