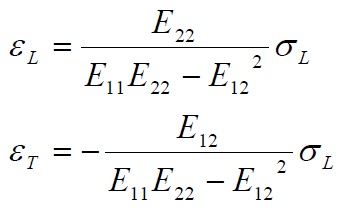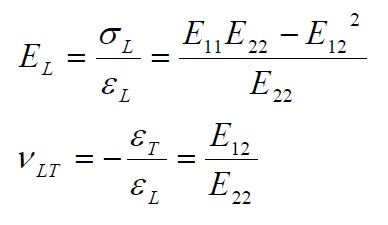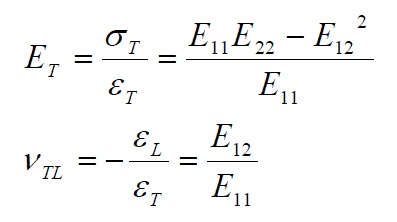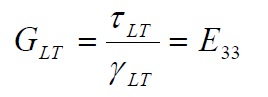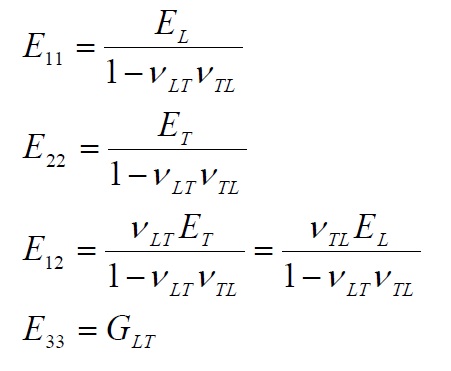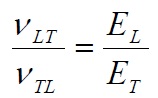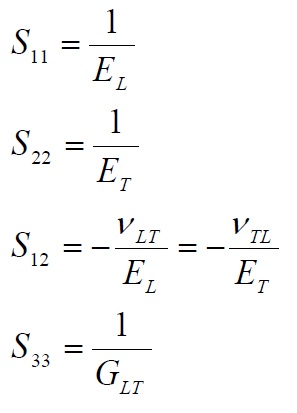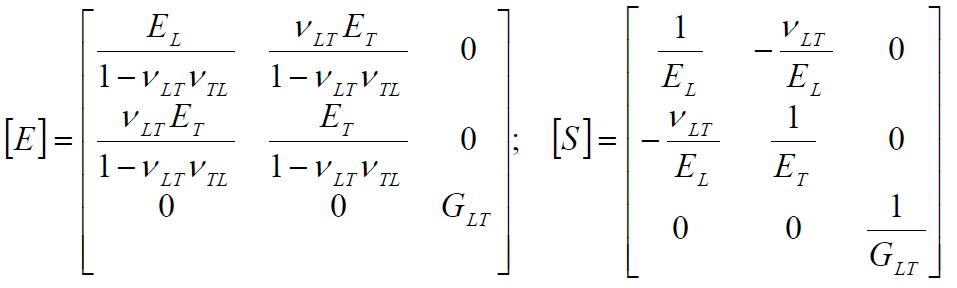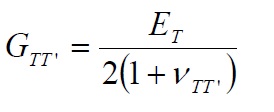1 . Analysis of the Orthotropic Lamina
1.1. Introduction
1.2. Hooke’s Law
1.3. Relationships between elastic constants and Matrix of Elasticity
1.4. Matrix of Elasticity
2. Classical theory of Laminates
2.1. Introduction
2.2. Basic Formulas
2.3. Laminate stiffener matrix
2.4. Calculation of Stress and deformation
2.5. Thermal Stress
2.6. Calculation of Elastic Constants
>> Composite Analysis Tool
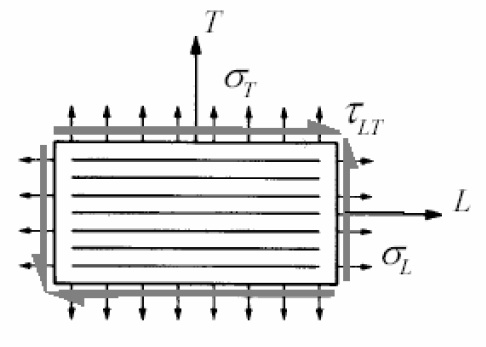
In the presence of a biaxial stress state, the mechanical behavior of a lamina orthotropic (Figure 3) is uniquely defined by the 4 constants EL, ET, GLT, νLT, (ν is not an independent parameter).
The relations between these elastic constants and the terms of the matrix of elasticity is obtained by considering the plate subjected to a uniaxial tension directed along the principal directions and for a state of pure shear. For a uniaxial stress along the longitudinal direction we have:
σL= E12 εL + E22 εT (11-12)
σT= E12 εL + E22 εT
that resolved with respect to deformations provide:
Thus taking account the definition of Young’s modulus and Poisson’s ratio, from the above equations we get:
Considering instead a uniaxial stress in the transverse direction, with the same procedure we obtain:
considering a pure shear stress, we have:
τLT= E33 γLT (19)
from which we obtain:
From the relationships (15-18) and (20) we therefore have:
According to (23), the two main Poisson ratios (major and minor) are in practice related to the Young’s modulus by the relation:
The result that of the 5 elastic constants present in the second member of (21-24) only 4 are independent. Using (21-24) and taking into account the relation (10) we obtain immediately the relations between the terms of the inverse matrix of elasticity and elastic constants:
Finally, in the planar case the matrix of elasticity direct and inverse assume the form:
For a orthotropic lamina, since it is also transversely isotropic (isotropic in the plane orthogonal to the longitudinal direction), in the three-dimensional case the independent elastic constants are not 9 as for a generic orthotropic, but only 5. Indicating with T ‘the direction orthogonal to the plane LT, it is easy to understand that it is:
ET’= ET ; GLT‘ = GLT ; νLT’ = νLT (31)
The transverse isotropy GTT’ is related to the Poisson’s ratio νTT’ and the Young’s modulus ET by the formula identical to that for the isotropic:
In the presence of three-dimensional states therefore, the analysis of the isotropic lamina requires the knowledge of five independent elastic constants. The elastic constants of the lamina may be obtained through tests or from the elastic constants of the fiber and matrix.