Rocket Propulsion:
– Thrust
– Combustion & Exhaust Velocity
– Staging
The specific impulse of a rocket, Isp, is the ratio of the thrust to the flow rate of the weight ejected, that is
![]()
where F is thrust, q is the rate of mass flow, and go is standard gravity (9.80665 m/s2). Specific impulse is expressed in seconds. When the thrust and the flow rate remain constant throughout the burning of the propellant, the specific impulse is the time for which the rocket engine provides a thrust equal to the weight of the propellant consumed. For a given engine, the specific impulse has different values on the ground and in the vacuum of space because the ambient pressure is involved in the expression for the thrust. It is therefore important to state whether specific impulse is the value at sea level or in a vacuum.
There are a number of losses within a rocket engine, the main ones being related to the inefficiency of the chemical reaction (combustion) process, losses due to the nozzle, and losses due to the pumps. Overall, the losses affect the efficiency of the specific impulse. This is the ratio of the real specific impulse (at sea level, or in a vacuum) and the theoretical specific impulse obtained with an ideal nozzle from gases coming from a complete chemical reaction. Calculated values of specific impulse are several percent higher than those attained in practice. From Equation (1.8) we can substitute qC for F in Equation (1.23), thus obtaining
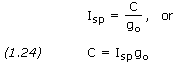
Equation (1.24) is very useful when solving Equations (1.18) through (1.21). It is rare we are given the value of C directly, however rocket engine specific impulse is a commonly given parameter from which we can easily calculate C.
Another important figure of merit for evaluating rocket performance is the characteristic exhaust velocity, C* (pronounced “C star”), which is a measure of the energy available from the combustion process and is given by
![]()
where Pc is the combustion chamber pressure and At is the area of the nozzle throat. Delivered values of C* range from about 1,333 m/s for monopropellant hydrazine up to about 2,360 m/s for cryogenic oxygen/hydrogen.
PROBLEM 1.6
A rocket engine produces a thrust of 1,000 kN at sea level with a propellant
flow rate of 400 kg/s. Calculate the specific impulse.
SOLUTION,
Given: F = 1,000,000 N
q = 400 kg/s
Equation (1.23),
Isp = F / (q × g)
Isp = 1,000,000 / (400 × 9.80665)
Isp = 255 s (sea level)