Orbit Meccanics:
- 1) Conic Sections
- 2) Orbital Elements
- 3) Types of Orbits
- 4) Newton’s Laws of Motion and Universal Gravitation
- 5) Uniform Circular Motion
- 6) Motions of Planets and Satellites
- 7) Launch of a Space Vehicle
- 8) Position in an Elliptical Orbit
- 9) Orbit Perturbations
- 10) Orbit Maneuvers
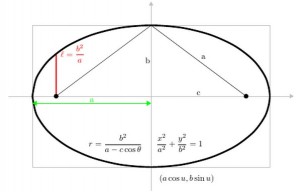
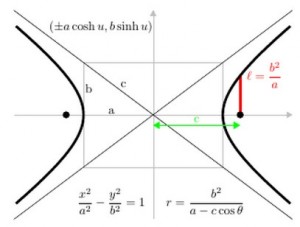
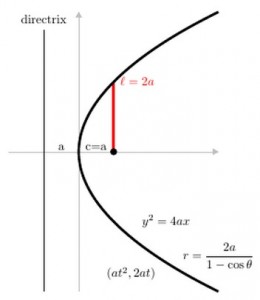
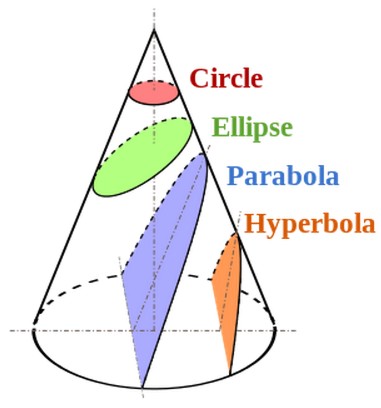
A conic section, or just conic, is a curve formed by passing a plane through a right circular cone. As shown in figure on the left, the angular orientation of the plane relative to the cone determines whether the conic section is a circle, ellipse, parabola, or hyerbola. The circle and the ellipse arise when the intersection of cone and plane is a bounded curve. The circle is a special case of the ellipse in which the plane is perpendicular to the axis of the cone. If the plane is parallel to a generator line of the cone, the conic is called a parabola. Finally, if the intersection is an unbounded curve and the plane is not parallel to a generator line of the cone, the figure is a hyperbola. In the latter case the plane will intersect both halves of the cone, producing two separate curves.
- Circle: (a cos θ, a sin θ)
- Ellipse: (a cos θ, b sin θ)
- Parabola: (at2, 2at)
- Hyperbola: (a sec θ, b tan θ) or (±a cosh u, b sinh u)
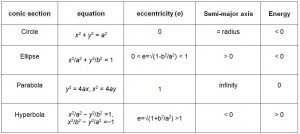
We can define all conic sections in terms of the eccentricity. The type of conic section is also related to the semi-major axis and the energy. The table above shows the relationships between eccentricity, semi-major axis, and energy and the type of conic section. Satellite orbits can be any of the four conic sections.